[reta] URGENTE!

por **mih123** » Seg Abr 01, 2013 21:01

Um quadrado ABCD tem a diagonal BD contida na reta r: x=1 ;y=z . Sabendo que A(0,0,0), determine os vértices B,C e D.

Valew.

por **e8group** » Ter Abr 02, 2013 01:31

Boa noite .

A reta

(interseção dos planos x= 1

e

)dada ,por sua configuração ,obtemos que se o segmento

(que é a diagonal do quadrado ) está contido em

temos que a tripla-ordenadas dos pontos

e

é solução da equação da reta

.Podemos tomar B = (1,b,b)

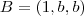e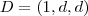

para algum

e

reais tais que

seja a diagonal do quadrado .

(OBS.:Faça um desenho do quadrado em questão para ilustrar a álgebra vetorial que iremos utlizar ).

Para encontrarmos o ponto

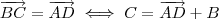,basta ver que os vetores $\overrightarrow{AD}$ e $\overrightarrow{BC}$ possuem a mesma direção (são paralelos) ,norma (comprimento) e o mesmo sentido ,isto é ,eles são iguais .Sendo assim , $\overrightarrow{BC} = \overrightarrow{AD} \iff C = \overrightarrow{AD} + B$ .Como foi dado que A=(0,0,0)

temos que $\overrightarrow{BC} = \overrightarrow{AD} \iff C = (2,b+d,b+d)$ .

Dica : Para concluir o exercício observe que assim como os lados do quadrado ,suas diagonais possuem o mesmo comprimento ,espero que consiga concluir ...

[reta] URGENTE!

[reta] URGENTE!

[reta] URGENTE!

Re: [reta] URGENTE!

Quem está online