Então, estava tentando resolver alguns exercicios e tive uma dificuldade específica em transformas a reta h para a forma vetorial, acho que depois disso eu conseguiria mais facilmente desenvolver a questão, então me ajudem por favor e se possível explanem a resolução.
obg
livro : Geometria Analítica - Um tratamento vetorial (Paulo Boulos)
problema: 20-22
Calcule a distância do ponto de interseção de r e s ao plano determinado por t e h, sendo
r: X = (1,3,4) + ?(1,2,3) s: X = (1,1,0) + ?(-1,0,1)
t: X = (0,1,0) + ?(0,6,1) h: x = y - 6z + 8 = 2x + 3
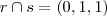(Por favor faça as contas ,se não conseguir post )
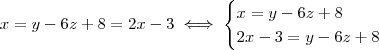
p/ algum t real .Obtemos que , 
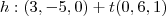. (Neste caso forma vetorial ) 
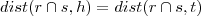será a distância do ponto 
ao plano em questão . 
teremos que o vetor 
será ortogonal ao plano procurado que chamemos de 
, onde : 
e 
são pontos quaisquer das respectivas retas t e h .Podemos por exemplo tomar , 
e 
. 
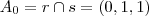ao plano 
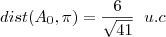
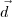é o vetor diretor de t ,h .
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.