Escreva uma equação do plano que contém o ponto (1,-2,3) e é perpendicular a cada um dos planos
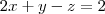 e
e  .
.Ao meu modo de ver, há duas soluções possíveis.
Uma delas é:
Os vetores normais
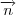 dos planos:
dos planos: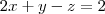
 =(2,1,-1) e
=(2,1,-1) e
 =(1,-1,-1) são paralelos ao plano que contém o ponto (1,-2,3). Se eu fizer
=(1,-1,-1) são paralelos ao plano que contém o ponto (1,-2,3). Se eu fizer  X
X  , vou obter um vetor normal ao plano que no qual quero encontrar a equação? Acredito que seja uma solução, mas ainda tenho minhas dúvidas. Estou certo?
, vou obter um vetor normal ao plano que no qual quero encontrar a equação? Acredito que seja uma solução, mas ainda tenho minhas dúvidas. Estou certo?O outro modo é:
Encontrar dois pontos pertencentes a um dos planos dados, por exemplo A(x,y,z) e B(x,y,z) e fazendo
 e este vetor
e este vetor  seria um vetor normal ao plano que quero encontrar sua equação.
seria um vetor normal ao plano que quero encontrar sua equação.Mas aí vai a pergunta:
Como encontrar dois pontos de um plano?


