Escreva uma equação do plano paralelo ao eixo z e que contém os pontos A(2,0,0) e B(0,3,2).
Sei que quando um plano é paralelo a um eixo, este eixo é zero na equação deste plano, mas o que eu posso retirar desta informação?
Eu faria assim:

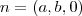

Sei que para achar o valor de d da equação do plano, eu deveria fazer:

portanto, temos:

Mas, como podem ver, há 3 variáveis... não sei o que fazer.
Escreva uma equação do plano paralelo ao eixo z e que contém o ponto (1,1,1)
Como eu havia dito, sei que na equação deste plano
 , mas não sei o que retirar desta informação para que eu possa relaciona-lo com este ponto dado.
, mas não sei o que retirar desta informação para que eu possa relaciona-lo com este ponto dado.


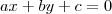 ? Por que o
? Por que o  foi retirado?
foi retirado?
 e
e 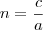
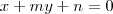
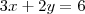 , ou seja,
, ou seja, 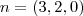 e
e  . Mas como achar este vetor n?
. Mas como achar este vetor n?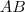 e
e  ,
, 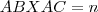 . E então?
. E então?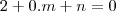



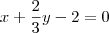


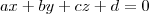 , como o plano é paralelo ao eixo z, temos:
, como o plano é paralelo ao eixo z, temos: , dividindo a equação por a:
, dividindo a equação por a:

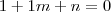
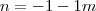
 ficou em função de
ficou em função de  , ou seja, se eu substituir o valor de
, ou seja, se eu substituir o valor de 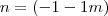 na equação do plano, temos:
na equação do plano, temos:
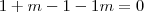


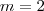 ;
;
 , esta seria a equação do plano?
, esta seria a equação do plano? .
.
 ou
ou  ou
ou  ?
? 

 , avisa que eu resolvo.
, avisa que eu resolvo.

