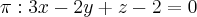 e intercepta a reta
e intercepta a reta 
Bem, sei que a equação da reta s será s: (0,0,0)+hv, sendo v o vetor diretor de s.
n é o vetor normal ao plano pi. n=(3,-2,1)
Se e é paralela a pi, então, v e n são perpendiculares.
Logo,
v.n=0.
E, se as retas s e r se cruzam é pq são concorrentes e tem um ponto de interseção.
Sei as informações, mas como usá-las para achar a equação de s, que é o meu objetivo???
Obrigada, desde já!


 (já que s é paralela a
(já que s é paralela a  ) . Facilmente você pode calcular que
) . Facilmente você pode calcular que  . Por outro lado, como P também é um ponto de r, você sabe que ele tem o formato
. Por outro lado, como P também é um ponto de r, você sabe que ele tem o formato  para algum escalar
para algum escalar 

 .
.
 :
: