 ao plano
ao plano 
Não consegui resolver esse exercício, mas o caminho seria projeção? Não encontrei a resposta correta, alguém teria alguma dica?
Analogamente vi um exercício pedindo o seguinte:
Determine a distância do ponto
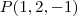 à reta
à reta 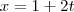 ;
; 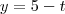 ;
; 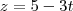 , seria da mesma forma que determinar distância de ponto ao plano?
, seria da mesma forma que determinar distância de ponto ao plano?

 o plano, escolhendo um ponto qualquer
o plano, escolhendo um ponto qualquer  , por exemplo
, por exemplo 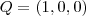
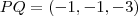
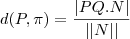
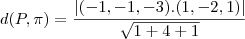
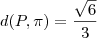

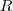 da reta, quando t = 0, teremos
da reta, quando t = 0, teremos 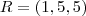
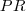 encontramos
encontramos 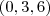 ou
ou 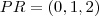

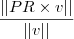
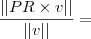
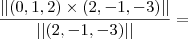
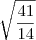
![\frac{3\sqrt[]{6}}{2} \frac{3\sqrt[]{6}}{2}](/latexrender/pictures/8f7f35bba80503cf6f621b5900b3bda8.png)
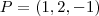 e
e 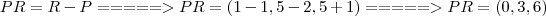
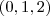
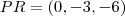 que dividido por - 3...
que dividido por - 3...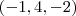 que multiplicado por - 3 dá
que multiplicado por - 3 dá 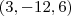
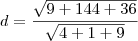
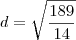
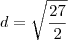
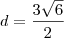

![\frac{\sqrt[]{27}}{\sqrt[]{2}}\Rightarrow \frac{\sqrt[]{27}}{\sqrt[]{2}}.\frac{\sqrt[]{2}}{\sqrt[]{2}}= \frac{3\sqrt[]{6}}{2} \frac{\sqrt[]{27}}{\sqrt[]{2}}\Rightarrow \frac{\sqrt[]{27}}{\sqrt[]{2}}.\frac{\sqrt[]{2}}{\sqrt[]{2}}= \frac{3\sqrt[]{6}}{2}](/latexrender/pictures/1017c11e8ba8b83ae5a2f0c2d5256438.png)

 .
.
 :
: