 por Danilo » Dom Mai 13, 2012 22:05
por Danilo » Dom Mai 13, 2012 22:05
Segue o exercício:
Dê a equação da reta suoprte de um segmento que tem centro P (0,3) e extremidade em cada uma das retas 2x -y -2 = 0 e x+y+3 = 0.
bom, eu fiz assim: Cada extremidade corresponde um ponto de cada reta. a reta 2x - y -2 = 0 passa pelo ponto R. e a outra reta pelo ponto S.
isolei o y em cada equação da reta e chamei a abscissa de XR, entao a ordenada ficou 2XR -2. e analogamente para a outra reta.
P é ponto medio da reta que passam os pontos. aí ficou: Xp = XR + XS/ 2
fazendo algumas contas cheguei a conclusão de que o ponto R = (11/3, 16/3) e o ponto S = (7/3, -16/3)
já que o ponto R e o ponto P estão na mesma reta eu tentei encontrar a equação da reta utilizando as coordenadas destes dois pontos. Mas o problema que não condiz com a resposta... já tentei usar as coordenadas de S mais a de P, e as de S e mais as R e não dá.
8x-y-24= 0 é a resposta.
Alguém poderia me dizer onde estou errando? Obrigado desde já!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 13:53
por LuizAquino » Seg Mai 14, 2012 13:53
Danilo escreveu:Dê a equação da reta suoprte de um segmento que tem centro P (0,3) e extremidade em cada uma das retas 2x -y -2 = 0 e x+y+3 = 0.
Danilo escreveu:bom, eu fiz assim: Cada extremidade corresponde um ponto de cada reta. a reta 2x - y -2 = 0 passa pelo ponto R. e a outra reta pelo ponto S.
isolei o y em cada equação da reta e chamei a abscissa de XR, entao a ordenada ficou 2XR -2. e analogamente para a outra reta.
P é ponto medio da reta que passam os pontos. aí ficou: Xp = XR + XS/ 2
fazendo algumas contas cheguei a conclusão de que o ponto R = (11/3, 16/3) e o ponto S = (7/3, -16/3)
Se você conferisse sua conclusão veria que ela está errada. Calculando (R+S)/2 não obtemos P como era esperado. Refaça suas contas e tente prosseguir.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Ter Mai 15, 2012 01:14
por Danilo » Ter Mai 15, 2012 01:14
LuizAquino escreveu:Danilo escreveu:Dê a equação da reta suoprte de um segmento que tem centro P (0,3) e extremidade em cada uma das retas 2x -y -2 = 0 e x+y+3 = 0.
Danilo escreveu:bom, eu fiz assim: Cada extremidade corresponde um ponto de cada reta. a reta 2x - y -2 = 0 passa pelo ponto R. e a outra reta pelo ponto S.
isolei o y em cada equação da reta e chamei a abscissa de XR, entao a ordenada ficou 2XR -2. e analogamente para a outra reta.
P é ponto medio da reta que passam os pontos. aí ficou: Xp = XR + XS/ 2
fazendo algumas contas cheguei a conclusão de que o ponto R = (11/3, 16/3) e o ponto S = (7/3, -16/3)
Se você conferisse sua conclusão veria que ela está errada. Calculando (R+S)/2 não obtemos P como era esperado. Refaça suas contas e tente prosseguir.
Professor, revi os cálculos e não encontrei erro nas coordenadas dos pontos.. O que vc quer dizer com ''não obtemos P como era esperado.'' Voce quer dizer que estou interpretando errado o resultado que encontrei? Obrigado
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Ter Mai 15, 2012 01:56
por Danilo » Ter Mai 15, 2012 01:56
Uma outra dúvida... os pontos R, S e P estão na mesma reta?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Ter Mai 15, 2012 11:52
por LuizAquino » Ter Mai 15, 2012 11:52
Danilo escreveu:Professor, revi os cálculos e não encontrei erro nas coordenadas dos pontos.. O que vc quer dizer com ''não obtemos P como era esperado.'' Voce quer dizer que estou interpretando errado o resultado que encontrei?
Do jeito que você fez sua resolução, o ponto P seria o ponto médio do segmento RS. Entretanto, note que:
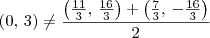
Ou seja, temos que P é diferente de (R+S)/2. Sendo assim, há um erro nos seus cálculos. Tente descobri-lo.
Danilo escreveu:Uma outra dúvida... os pontos R, S e P estão na mesma reta?
Se você encontrar os pontos R e S corretos, então R, S e P estarão sobre uma mesma reta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Ter Mai 15, 2012 23:43
por Danilo » Ter Mai 15, 2012 23:43
Professor, me desculpa! Na verdade o ponto P é (3,0) e não (0,3). Realmente fiz certinho ^^. Mas o problema é que não consigo encontrar a equação da reta correta (de acordo com a resposta.) tendo esses pontos.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Qua Mai 16, 2012 01:19
por Danilo » Qua Mai 16, 2012 01:19
Professor, consegui chegar na equação! Pensei certinho... todo o problema foi a álgebra e a confusão que eu fiz com o enunciado. Obrigado pela elucidação.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício sobre equação da reta - Dúvida
 por Danilo » Seg Mai 07, 2012 00:28
por Danilo » Seg Mai 07, 2012 00:28
- 2 Respostas
- 1933 Exibições
- Última mensagem por Danilo

Dom Mai 13, 2012 22:38
Geometria Analítica
-
- Dúvida em exercício - Equação da reta
 por Danilo » Qui Mai 24, 2012 05:11
por Danilo » Qui Mai 24, 2012 05:11
- 5 Respostas
- 3931 Exibições
- Última mensagem por Danilo

Sáb Mai 26, 2012 18:59
Geometria Analítica
-
- Duvida em exercício {equação da reta/perpendicularismo}
por Danilo » Qui Jun 14, 2012 06:15
- 2 Respostas
- 1832 Exibições
- Última mensagem por Danilo

Sáb Jun 16, 2012 03:22
Geometria Analítica
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7710 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- interseção,área e reta dúvida exercício
por igor44 » Seg Out 31, 2011 21:20
- 1 Respostas
- 2119 Exibições
- Última mensagem por procyon

Ter Nov 01, 2011 00:57
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
