 por Claudin » Qui Abr 05, 2012 19:19
por Claudin » Qui Abr 05, 2012 19:19
Mostre que os pontos (0,1,-1), (1,3,0) e (2,5,1) são colineares.
Também não consegui resolver esse exercício, fiz um com dois pontos, ai fiz uma relação de proporcionalidade entre os pontos e deu certo.
Agora com os três pontos não deu certo.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lucio Carvalho » Qui Abr 05, 2012 20:06
por Lucio Carvalho » Qui Abr 05, 2012 20:06
Olá Claudin,
se os pontos A, B e C são colineares, os vetores AB e BC (nota: falta a seta) terão de ter a mesma direção, ou seja, terão de ser colineares.
vetor AB = B - A = (1,3,0) - (0,1,-1) = (1,2,1)
vetor BC = C - B = (2,5,1) - (1,3,0) = (1,2,1)
Se os vetores têm a mesma direção, existe um

tal que:
vetor AB =

.(vetor BC)
(1,2,1) =

.(1,2,1)
Logo,

=1
Resposta: Os pontos são colineares.
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por LuizAquino » Qui Abr 05, 2012 21:22
por LuizAquino » Qui Abr 05, 2012 21:22
Lucio Carvalho escreveu:os vetores AB e BC (nota: falta a seta)
Para inserir as setas (bem como as outras notações matemáticas), use o LaTeX. Por favor, vide o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74No caso dos vetores, basicamente há duas formas de inserir as setas.
Forma 1)Use o código:
- Código: Selecionar todos
[tex]\vec{AB}[/tex]
Resultado:
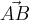 Forma 2)
Forma 2)Use o código:
- Código: Selecionar todos
[tex]\overrightarrow{AB}[/tex]
Resultado:
 Observação
ObservaçãoNote que a
Forma 1) é mais interessante de ser usada quando temos apenas uma letra em minúsculo:

. Já a
Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Abr 05, 2012 22:31
por Claudin » Qui Abr 05, 2012 22:31
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pontos Não-Colineares
 por wilgaroto » Sex Out 28, 2011 09:41
por wilgaroto » Sex Out 28, 2011 09:41
- 1 Respostas
- 4451 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:51
Geometria Analítica
-
- Pontos P,Q e R - Colineares ?
por PeterHiggs » Seg Set 24, 2012 19:10
- 2 Respostas
- 2449 Exibições
- Última mensagem por PeterHiggs

Ter Set 25, 2012 13:18
Geometria Espacial
-
- Pontos colineares
por Milton21 » Qui Out 18, 2012 15:14
- 4 Respostas
- 15811 Exibições
- Última mensagem por e8group

Sex Out 19, 2012 17:48
Geometria Analítica
-
- Duvida Pontos Colineares
por samuel_corf » Seg Abr 25, 2011 11:51
- 4 Respostas
- 9495 Exibições
- Última mensagem por LuizAquino

Dom Jul 24, 2011 20:46
Matrizes e Determinantes
-
- Combinaçao com elementos colineares
por rsholtermann » Qua Jul 14, 2010 13:21
- 1 Respostas
- 3048 Exibições
- Última mensagem por MarceloFantini

Qua Jul 14, 2010 14:50
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 tal que:
tal que: .(vetor BC)
.(vetor BC) .(1,2,1)
.(1,2,1) =1
=1
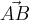

 . Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:
. Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:  .
.
