[Dependência Linear] Exercício do Boulos

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Dependência Linear] Exercício do Boulos

Regras do fórum
Responder

[Dependência Linear] Exercício do Boulos

Mensagempor Vinicius Rodrigues » Dom Abr 01, 2012 01:52

Suponha que (\vec{u}, \vec{v}, \vec{w}) seja LI. Dado \vec{t}, existem \alpha, \beta e \gamma tais que \vec{t}=\alpha\vec{u}+\beta\vec{v}+\gamma\vec{w}.
Prove:

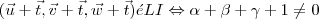
Tentei a ida primeiro.

Certo, creio que o caminho seja avaliar as soluções de
x(\vec{u})+\vec{t})+y(\vec{v})+\vec{t})+\z(\vec{w})+\vec{t})=\vec(0)

Substituindo \vec{t}=\alpha\vec{u}+\beta\vec{v}+\gamma\vec{w} e desenvolvendo, colocando u, v e w em evidência, chego em:
x(a+1)+ya+za=0
y(b+1)+yb+zb=0
z(c+1)+yc+zc=0
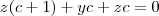
Empaco aí. não consigo chegar em um meio de mostrar que a soma de a, b e c deve ser diferente de -1.
Alguma sugestão?
Editado pela última vez por Vinicius Rodrigues em Dom Abr 01, 2012 03:42, em um total de 1 vez.
Vinicius Rodrigues
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Dom Abr 01, 2012 01:22
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo

Re: [Dependência Linear] Exercício do Boulos

Mensagempor MarceloFantini » Dom Abr 01, 2012 03:32

Vinícius, por favor leia as regras do fórum, em especial a primeira.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: [Dependência Linear] Exercício do Boulos

Mensagempor Vinicius Rodrigues » Dom Abr 01, 2012 03:43

Desculpe-me. Editei. Amanhã coloco mais detalhes, agora estou caindo de sono. Obrigado ^^.
Vinicius Rodrigues
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Dom Abr 01, 2012 01:22
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Geometria Analítica

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum