 por Andreza » Sáb Fev 25, 2012 09:43
por Andreza » Sáb Fev 25, 2012 09:43
Qual é a equação da circunferência que circunscreve o triângulo equilátero ABC, cujo lado mede 4
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
Eu consegui achar a altura q deu 6 unidades mas não consigo relacionar ela com a fórmula.
Desde já agradeço qualquer ajuda ou dica.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por Guill » Sáb Fev 25, 2012 11:43
por Guill » Sáb Fev 25, 2012 11:43
Imaginando uma circunferência que circunscreve um triângulo equilátero de lado
![4.\sqrt[]{3} 4.\sqrt[]{3}](/latexrender/pictures/c0444245f15b6b85ccd929e0e777238c.png)
, veremos que essa circunferência toca cada lado do triângulo, portanto esses lados são tângentes da circunferência.
A altura dessa triângulo é a bissetriz e a mediana, além de passarem pelo centro da circunferência:
![h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2 h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2](/latexrender/pictures/d3ea7129b6d43fd44b0f7baea8bf9b5a.png)
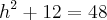

Sabendo a altura, e sabendo que ela faz parte do eixo y, sabemos que o centro da circunferência também está no eixo y. Agora, se traçarmos, a partir do centro dessa circunferênca, um segmento até o vértice e outro até o lado tangente, teremos um triângulo retângulo, onde o ângulo oposto ao raio é de 30º. Dessa forma, descobrimos que o segmento do centro ao vértice é 2 vezes maior que o segmento do centro à tangente. Como a soma desses comprimentos me dá a altura do triângulo:
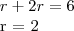
O problema é que não existem informações acerca da posição do triângulo no eixo y. Dessa forma, não podemos saber onde a altura começa ou termina. Mas sabemos que a equação é do tipo:
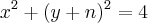
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação da Circunferência
por Cleyson007 » Qui Abr 08, 2010 15:35
- 1 Respostas
- 11146 Exibições
- Última mensagem por davi_11

Dom Abr 11, 2010 13:46
Geometria Analítica
-
- Equação da circunferência
por PedroSantos » Dom Jan 09, 2011 16:38
- 3 Respostas
- 2194 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 12:18
Geometria Plana
-
- Equação na Circunferência
por Fernandobertolaccini » Dom Mai 11, 2014 14:48
- 1 Respostas
- 1238 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:26
Geometria Analítica
-
- Equação da circunferencia
por brunoguim05 » Qua Mai 28, 2014 15:20
- 1 Respostas
- 1276 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:15
Equações
-
- Equação da circunferência
por YuriFreire » Seg Ago 25, 2014 23:22
- 2 Respostas
- 1368 Exibições
- Última mensagem por YuriFreire

Ter Ago 26, 2014 22:30
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
![4.\sqrt[]{3} 4.\sqrt[]{3}](/latexrender/pictures/c0444245f15b6b85ccd929e0e777238c.png) , veremos que essa circunferência toca cada lado do triângulo, portanto esses lados são tângentes da circunferência.
, veremos que essa circunferência toca cada lado do triângulo, portanto esses lados são tângentes da circunferência.![h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2 h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2](/latexrender/pictures/d3ea7129b6d43fd44b0f7baea8bf9b5a.png)
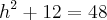

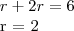
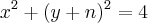



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.