por Andreza » Qui Jan 26, 2012 11:59
Qual a equação da elipse de focos F1=(-1,0) e F2=(1,0) e eixo maior igual a 8?
Qual fórmula eu uso para encontrar a equação reduzida?
Desde já agradeço.
-
Andreza
- Colaborador Voluntário
-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
por LuizAquino » Qui Jan 26, 2012 12:06
Andreza escreveu:Qual a equação da elipse de focos F1=(-1,0) e F2=(1,0) e eixo maior igual a 8?
Qual fórmula eu uso para encontrar a equação reduzida?
Use a relação entre a distância focal e os coeficientes a e b da equação
.
Leia a página abaixo.
Elipsehttp://pt.wikipedia.org/wiki/Elipse
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
por Andreza » Qui Jan 26, 2012 13:37
Eu encontrei q a=4
Substituindo em a²=b²+c²
Encontrei b²=15
Portanto a equação seria:
?
-
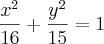
Andreza
- Colaborador Voluntário
-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
por LuizAquino » Qui Jan 26, 2012 14:01
Andreza escreveu:Eu encontrei q a=4
Substituindo em a²=b²+c²
Encontrei b²=15
Portanto a equação seria:
?
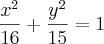
Você mesmo pode conferir a sua resposta! Basta seguir o caminho contrário!
Considerando a equação da elipse que você encontrou, determine o eixo maior e os focos. Se você obter que o eixo maior mede 8 e que os focos são F1=(-1, 0) e F2=(1, 0), então a sua resposta está correta!
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação de uma elipse
por max » Dom Mar 20, 2011 18:44
- 2 Respostas
- 1781 Exibições
- Última mensagem por max
Dom Mar 20, 2011 22:01
Geometria Analítica
-
- Equação da elipse
por marinalcd » Qui Ago 23, 2012 19:14
- 1 Respostas
- 1184 Exibições
- Última mensagem por MarceloFantini
Qui Ago 23, 2012 20:29
Geometria Analítica
-
- Equação da elipse
por marcos machado » Sáb Mai 31, 2014 13:57
- 1 Respostas
- 1167 Exibições
- Última mensagem por DanielFerreira
Sáb Jul 05, 2014 16:21
Geometria Analítica
-
- Equacao para elipse
por jmontenegro » Ter Fev 28, 2012 14:56
- 3 Respostas
- 2318 Exibições
- Última mensagem por LuizAquino
Qua Fev 29, 2012 02:23
Geometria Analítica
-
- (CONICAS) equação da elipse
por manuel_pato1 » Sáb Nov 17, 2012 20:53
- 4 Respostas
- 2690 Exibições
- Última mensagem por manuel_pato1
Qua Nov 21, 2012 20:44
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
