Oi pessoal, como vão.
To estudando Geometria Analítica na facul e to com dificuldade de descobrir um vetor normal a um plano dado. Como fazer isso se eu tiver a equação vetorial de um plano? Eu li alguma coisa sobre colocar a equação na forma geral e assim pegar os coeficientes dela.
Ex: 2x+5y+z+2=0
aí o vetor seria:
(2,5,1)
É isso mesmo ou tem outro modo?
Até mais e obrigado desde ja


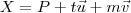 , sendo
, sendo  e
e  são chamados de
são chamados de  é um vetor normal ao plano dado pela equação anterior, então
é um vetor normal ao plano dado pela equação anterior, então  e
e  .
.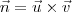 .
.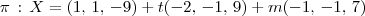 .
.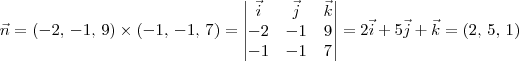 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)