 por Florisbela » Dom Mai 23, 2010 19:22
por Florisbela » Dom Mai 23, 2010 19:22
Boa noite!
Preciso de ajuda para resolver este aqui:

-
Florisbela
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 23, 2010 19:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão Ambiental
- Andamento: cursando
 por Neperiano » Dom Mai 23, 2010 19:48
por Neperiano » Dom Mai 23, 2010 19:48
Ola
Esta é uma equação biquadradica
Esta equação pode ser reduzida a uma equação do segundo grau através seguinte mudança de variáveis:
x=q^2
Substituindo
x^2-13x+36
Utilize bascara e resolva
Espero ter ajudado
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Florisbela » Dom Mai 23, 2010 20:08
por Florisbela » Dom Mai 23, 2010 20:08
Caramba.... Agora ficou fácil... Ajudou muito mesmo. Obrigada!
-
Florisbela
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 23, 2010 19:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão Ambiental
- Andamento: cursando
 por MarceloFantini » Seg Mai 24, 2010 21:35
por MarceloFantini » Seg Mai 24, 2010 21:35
Mas não se esqueça que como você definiu que

, pode ser que alguns valores de x não realmente satisfaçam a equação (
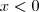
por exemplo). Lembre-se que o que você quer são as soluções de

, e não de

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8350 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
-
- GRAU DE POLINOMIOS
por Lismara » Qua Set 16, 2009 22:18
- 8 Respostas
- 6618 Exibições
- Última mensagem por cristina

Qua Set 23, 2009 00:05
Polinômios
-
- raizes de polinomios de grau 3
por theSinister » Seg Mai 09, 2011 17:58
- 9 Respostas
- 5453 Exibições
- Última mensagem por theSinister

Seg Mai 09, 2011 21:35
Álgebra Elementar
-
- Simplificação do quociante de polinômios de quarto grau
por Caroline Oliveyra » Qui Jun 23, 2011 22:19
- 4 Respostas
- 3999 Exibições
- Última mensagem por Caroline Oliveyra

Qui Jun 23, 2011 23:36
Polinômios
-
- Equações de 1 grau e 2 grau
por Neperiano » Sex Out 10, 2008 22:22
- 7 Respostas
- 13954 Exibições
- Última mensagem por DanielFerreira

Dom Jul 26, 2009 12:55
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 , pode ser que alguns valores de x não realmente satisfaçam a equação (
, pode ser que alguns valores de x não realmente satisfaçam a equação (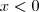 por exemplo). Lembre-se que o que você quer são as soluções de
por exemplo). Lembre-se que o que você quer são as soluções de  , e não de
, e não de  .
.

