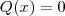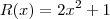por Cleyson007 » Sex Jan 22, 2010 18:12
por Cleyson007 » Sex Jan 22, 2010 18:12
Boa tarde!
Estou meio perdido quanto a resolução do problema abaixo.
Segue exercício:
Determine, usando a divisão euclidiana, o quociente q(x) e o resto r(x) da divisão de f(x) por g(x):
f(x) = 2x² + 1, g(x) = x³ + 2x² - 1
--> Gostaria de saber se a "Divisão Euclidiana" é a mesma do "Método da Chave". Outra dúvida é a seguinte: como dividir um polinômio de grau menor por outro de grau maior?
Agradeço a atenção!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Sex Jan 22, 2010 20:30
por Molina » Sex Jan 22, 2010 20:30
Cleyson007 escreveu:Boa tarde!
Estou meio perdido quanto a resolução do problema abaixo.
Segue exercício:
Determine, usando a divisão euclidiana, o quociente q(x) e o resto r(x) da divisão de f(x) por g(x):
f(x) = 2x² + 1, g(x) = x³ + 2x² - 1
--> Gostaria de saber se a "Divisão Euclidiana" é a mesma do "Método da Chave". Outra dúvida é a seguinte: como dividir um polinômio de grau menor por outro de grau maior?
Agradeço a atenção!
Boa noite, Cleyson.
É isso mesmo. O método da divisão euclidiana é o uso de chaves, assim como se faz com um número natural.
Agora quanto a divisao de um polinômio de grau menor pelo de um grau maior é difícil de se ver. O que eu faria neste caso é usar potências negativas, ex:

Você tem o gabarito?
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sáb Jan 23, 2010 22:00
por MarceloFantini » Sáb Jan 23, 2010 22:00
Boa noite.
Acredito que isto não seja possível, pois pelo o que me recordo um polinômio precisa ter expoentes inteiros e maiores que um.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Sáb Jan 23, 2010 22:26
por Cleyson007 » Sáb Jan 23, 2010 22:26
Boa noite Molina e Fantini!
Fiz a questão de postar esse exercício pelo fato de tê-lo achado estranho (eu também nunca havia visto tal fato).
Molina, não tenho o gabarito da questão.. tentei fazer pelo caminho que me aconselhou, mas também não obtive resultado.
Agradeço a ajuda dos dois.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Sáb Jan 23, 2010 22:30
por MarceloFantini » Sáb Jan 23, 2010 22:30
Cleyson, acredito que a resposta seja:
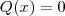
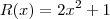
Um abraço.
P.S.: Gostaria de pegar o seu MSN pra conversamos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LÓGICA, DIVISÃO EUCLIDIANA]
por juliohenriquelima14 » Seg Dez 15, 2014 10:02
- 1 Respostas
- 1673 Exibições
- Última mensagem por adauto martins

Qua Dez 17, 2014 15:10
Aritmética
-
- Euclidiana
por apotema2010 » Sex Mai 07, 2010 15:03
- 2 Respostas
- 1332 Exibições
- Última mensagem por apotema2010

Sex Mai 07, 2010 15:57
Geometria Plana
-
- Geometria Euclidiana
por Caeros » Seg Mai 25, 2009 19:13
- 1 Respostas
- 2018 Exibições
- Última mensagem por Caeros

Seg Mai 25, 2009 19:33
Geometria Plana
-
- Geometria Euclidiana
por rheilagouveia » Sex Mai 21, 2010 02:25
- 1 Respostas
- 3582 Exibições
- Última mensagem por MarceloFantini

Sex Mai 21, 2010 14:15
Apresentação dos Participantes
-
- Geometria Euclidiana
por _Jane » Sex Abr 05, 2013 15:56
- 2 Respostas
- 1678 Exibições
- Última mensagem por _Jane

Sáb Abr 06, 2013 00:48
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.