 por ftdk » Dom Set 23, 2012 10:17
por ftdk » Dom Set 23, 2012 10:17
Bom dia.
" Determine pelo metodo de Laguerre o intervalo que contenha todas as raizes reais da equacao

"
Exercicio relativamente simples, mas ao fazer a aproximacao da raiz, me deparei com nosso amigo
zero. Minha duvida é se, nesse caso, eu devo coloca-lo em uma classificacao de
positivo ou
negativo apenas para terminar a resolucao, e lembrando que eu ainda nao conheço numeros complexos, mas o enunciado pediu apenas as raizes reais.
Até este momento, o resultado bate com o gabarito, pois o intervalo é ]-2;2[. Mas, se fosse necessário, como eu deveria proceder nessa situação ?

ps: tentei postar sem utilizar imagens externas, mas nao consegui inserir tabelas aqui. Existe algum tutorial para insercao de tabelas?
-
ftdk
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Set 23, 2012 09:31
- Localização: Sao Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eletrônica
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 13:34
por MarceloFantini » Dom Set 23, 2012 13:34
Não entendo o que quer dizer exatamente, pois zero não é uma raíz deste polinômio. O que acontece é que o valor da função é negativo neste ponto. Marque apenas como raíz, não precisa classificá-lo como positivo ou negativo (mesmo porque ele é neutro).
Você poderia usar LaTeX para inserir a tabela.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ftdk » Dom Set 23, 2012 15:05
por ftdk » Dom Set 23, 2012 15:05
Marcelo, obrigado pela resposta e desculpe se nao fui bem claro.
De acordo com o metodo de Laguerre, ao substituirmos os valores do intervalo ]-2;2[ na função, sempre que o resultado alternar entre + e -, significa que existe uma raiz real entre esses valores, correto? Por exemplo, existe 1 raiz real no intervalo ]1;2[
A minha duvida é quando substituo -1 na funcao. O resultado de f[-1] = 0, entao nao sei se em f[-1] eu considero positivo (acarretando em 1 raiz real entre ]-2;-1[, e 1 raiz real entre ]-1;0[ ) ou negativo (nao haveria nenhuma raiz real nesses intervalos).
-
ftdk
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Set 23, 2012 09:31
- Localização: Sao Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eletrônica
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 15:39
por MarceloFantini » Dom Set 23, 2012 15:39
Você está confundindo conceitos. A definição de raíz de uma função é justamente que
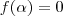
. Quando você substitui -1 na função você vê que

, logo -1 é raíz da função. Isto significa que qualquer intervalo contendo -1 fará com que a função assuma valores positivos e negativos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ftdk » Dom Set 23, 2012 18:24
por ftdk » Dom Set 23, 2012 18:24
Ah, então acho que tambem entendi porque não incluimos os extremos no intervalo ]-2;2[.
Agora, só por curiosidade, vou tentar calcular a menor e a maior raiz desse polinomio. Obrigado pela ajuda.
-
ftdk
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Set 23, 2012 09:31
- Localização: Sao Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eletrônica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Método dos Mínimos Quadrados - Dúvida no desenvolvimento
por cafdesouza » Dom Dez 11, 2011 11:36
- 0 Respostas
- 1267 Exibições
- Última mensagem por cafdesouza

Dom Dez 11, 2011 11:36
Estatística
-
- [Método de Newton] - Duvida nessa questão
por zifles2012 » Seg Set 17, 2012 16:13
- 1 Respostas
- 2127 Exibições
- Última mensagem por LuizAquino

Seg Set 17, 2012 19:55
Cálculo Numérico e Aplicações
-
- método de contagem
por sinuca147 » Seg Mai 25, 2009 09:10
- 2 Respostas
- 54377 Exibições
- Última mensagem por sinuca147

Seg Mai 25, 2009 23:35
Conjuntos
-
- Metodo de Gauss
por Jaison Werner » Seg Jan 10, 2011 19:11
- 3 Respostas
- 2986 Exibições
- Última mensagem por Renato_RJ

Ter Jan 18, 2011 23:42
Cálculo: Limites, Derivadas e Integrais
-
- Metodo de Jacobi
por Jaison Werner » Seg Jan 10, 2011 19:14
- 1 Respostas
- 1312 Exibições
- Última mensagem por Elcioschin

Ter Jan 11, 2011 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 "
"




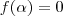 . Quando você substitui -1 na função você vê que
. Quando você substitui -1 na função você vê que  , logo -1 é raíz da função. Isto significa que qualquer intervalo contendo -1 fará com que a função assuma valores positivos e negativos.
, logo -1 é raíz da função. Isto significa que qualquer intervalo contendo -1 fará com que a função assuma valores positivos e negativos.