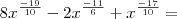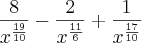[fatoração de polinômios]

por **jvabatista** » Qua Abr 18, 2012 01:42

Olá.

Estou com problemas para resolver isto:

$\frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}}$

**Divida, deixando aparecer somente expoentes positivos

Separei cada membro de cima com o mesmo denominador, dividi cada um dos três separadamente e encontrei isto:

$\frac{8}{{x}^{\frac{3}{5}}}-\frac{2}{{x}^{\frac{11}{6}}}+\frac{1}{{x}^{\frac{17}{10}}}$

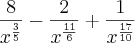
Não sei como simplificar mais do que isso e a resposta no livro é $8{x}^{\frac{2}{5}}-2{x}^{\frac{7}{5}}+{x}^{\frac{3}{5}}$ .

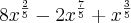Tentei resolver pelo método das chaves mas obtive o mesmo resultado. Há algum outro método para se chegar ao resultado do livro ou algo mais a simplificar de até onde calculei ?

por **DanielFerreira** » Qua Abr 18, 2012 23:08

$\frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} =$

$\frac{8x^{\frac{3}{5}} - 2x^{\frac{2}{3}} + x^{\frac{4}{5}}}{x^{\frac{5}{2}}}} =$

Aplicando MMC vamos deixar os denominadores iguais:

$\frac{8x^{\frac{18}{30}} - 2x^{\frac{20}{30}} + x^{\frac{24}{30}}}{x^{\frac{75}{30}}}} =$

Acho que agora vc consegue, tente!

Qualquer dúvida retorne.

por **jvabatista** » Qui Abr 26, 2012 17:49

Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:

$\frac{8{x}^{\frac{18}{30}}}{{x}^{\frac{75}{30}}}-\frac{{x}^{\frac{20}{30}}}{{x}^{\frac{75}{30}}}+\frac{{x}^{\frac{24}{30}}}{{x}^{\frac{75}{30}}}$ .

Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?

por **DanielFerreira** » Qui Abr 26, 2012 20:13

jvabatista escreveu:Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:

$\frac{8{x}^{\frac{18}{30}}}{{x}^{\frac{75}{30}}}-\frac{{x}^{\frac{20}{30}}}{{x}^{\frac{75}{30}}}+\frac{{x}^{\frac{24}{30}}}{{x}^{\frac{75}{30}}}$ .

Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?

Você esqueceu de colocar o 2 (termo negativo).

por **jvabatista** » Qui Abr 26, 2012 20:52

Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.

por **DanielFerreira** » Qui Abr 26, 2012 21:15

jvabatista escreveu:Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.

Então vamos a ela.
$\frac{8x^\frac{18}{30} - 2x^\frac{20}{30} + x^\frac{24}{30}}{x^\frac{75}{30}} =$

Pelo que entendi até aqui tudo bem, certo?!

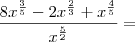
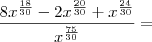
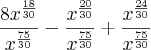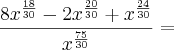
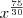Então, coloque $x^\frac{75}{30}$ em evidência, veja:

$\frac{x^\frac{75}{30}( 8x^\frac{- 57}{30} - 2x^\frac{- 55}{30} + x^\frac{- 51}{30})}{x^\frac{75}{30}} =$

$8x^\frac{- 19}{10} - 2x^\frac{- 11}{6} + x^\frac{- 17}{10} =$

ou

$\frac{8}{x^\frac{19}{10}} - \frac{2}{x^\frac{11}{6}} + \frac{1}{x^\frac{17}{10}}$

também encontrou isso?

por **jvabatista** » Qui Abr 26, 2012 21:27

Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.

por **DanielFerreira** » Dom Abr 29, 2012 00:42

jvabatista escreveu:Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.

De acordo!

[fatoração de polinômios]

[fatoração de polinômios]

[fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Re: [fatoração de polinômios]

Quem está online