 por emsbp » Sex Ago 03, 2012 18:10
por emsbp » Sex Ago 03, 2012 18:10
Boa tarde. É pedido para demonstrar a seguinte igualdade:
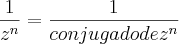
. (Peço desculpa, mas não consegui encontrar o símbolo de conjugado no editor).
Comecei por atribuir
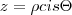
, donde

=

. Donde o seu conjugado será
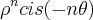
. Para
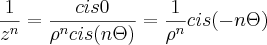
. Procedi do mesmo modo para o outro quociente e obtive

. No entanto, os ângulos são diferentes. O que me está a escapar?
Obrigado.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por MarceloFantini » Sex Ago 03, 2012 18:46
por MarceloFantini » Sex Ago 03, 2012 18:46
Tem certeza da igualdade? Tome

, então
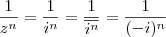
, que não é verdadeiro para todo

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por emsbp » Sex Ago 03, 2012 19:17
por emsbp » Sex Ago 03, 2012 19:17
No manual vem tal e qual como apresentei. Também estranhei.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- N° Complexos - Conjugado
por iceman » Seg Mai 28, 2012 19:52
- 6 Respostas
- 3763 Exibições
- Última mensagem por joaofonseca

Qua Mai 30, 2012 17:15
Números Complexos
-
- conjugado e simétrico
por anamendes » Sáb Mai 19, 2012 07:54
- 1 Respostas
- 1694 Exibições
- Última mensagem por emsbp

Sex Ago 03, 2012 18:21
Números Complexos
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25702 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17102 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5890 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
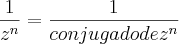 . (Peço desculpa, mas não consegui encontrar o símbolo de conjugado no editor).
. (Peço desculpa, mas não consegui encontrar o símbolo de conjugado no editor).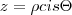 , donde
, donde  =
=  . Donde o seu conjugado será
. Donde o seu conjugado será 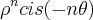 . Para
. Para 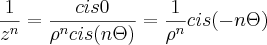 . Procedi do mesmo modo para o outro quociente e obtive
. Procedi do mesmo modo para o outro quociente e obtive  . No entanto, os ângulos são diferentes. O que me está a escapar?
. No entanto, os ângulos são diferentes. O que me está a escapar?

 , então
, então 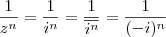 , que não é verdadeiro para todo
, que não é verdadeiro para todo  .
.
