 por gustavowelp » Sex Nov 19, 2010 09:02
por gustavowelp » Sex Nov 19, 2010 09:02
Bom dia.
Não sei nem como começar esta questão...
A primeira probabilidade já me confundiu... Ainda tem a segunda!
Uma urna contém 2 bolas brancas e 3 bolas amarelas distinguíveis apenas pela cor. Aleatoriamente, duas bolas serão escolhidas, sucessivamente e sem reposição, e colocadas em uma segunda urna, na qual há apenas uma bola preta também distinta das demais apenas pela cor. Após a transferência das duas bolas para a segunda urna, escolher-se-á, aleatoriamente, uma única bola dessa urna. Qual a probabilidade de que, nesse último sorteio, a bola escolhida seja amarela?
A resposta correta é: 0,40
Agradeço desde já!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 12:46
por alexandre32100 » Sex Nov 19, 2010 12:46
Escolhemos duas bolas dentre as cinco:
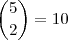
maneiras.
Daí formulamos as seguintes probabilidades:
- Escolher duas bolas brancas:
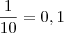
- Escolher duas bolas amarelas*:
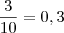
- Escolher uma bola de cada cor:

* esse número

é resultado da escolha de duas bolas dentre as três amarelas existentes na urna,
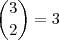
.
Se escolhermos duas amarelas na 1ª urna, a chance de retirar uma amarela na 2ª urna é de

, assim temos uma probabilidade de
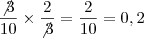
.
Agora, se na primeira urna escolhermos uma bola de cada cor, a possibilidade é de apenas

na segunda, ou ainda,

.
Por fim, chegamos ao resultado
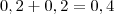
.
-
alexandre32100
-
 por gustavowelp » Sex Nov 19, 2010 13:04
por gustavowelp » Sex Nov 19, 2010 13:04
Não entendi o teu primeiro argumento
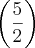
...
Seria combinação, certo?
Mas 1/10 quer dizer que somente há uma forma de retirar bolas brancas?
Obrigado!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 13:25
por alexandre32100 » Sex Nov 19, 2010 13:25
gustavowelp escreveu:Não entendi o teu primeiro argumento
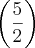
...
Seria combinação, certo?
Exato!
Eu uso a notação

, mas isto é o mesmo que

ou

.
Neste caso não fiz nada mais do que "escolher dois elementos dentre cinco", ou seja, combinação de cinco elementos tomados dois a dois.
gustavowelp escreveu:Mas 1/10 quer dizer que somente há uma forma de retirar bolas brancas?
Sim. Há duas bolas brancas na urna, ou seja, minha única forma de retirar duas bolas brancas é escolher estas únicas, ou ainda,

, diferente do caso das bolas amarelas (

,

e
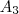
), onde eu posso formar três pares:

.
-
alexandre32100
-
 por gustavowelp » Sex Nov 19, 2010 13:34
por gustavowelp » Sex Nov 19, 2010 13:34
A dúvida que tenho é que as bolas brancas (ou amarelas) poderiam ser retiradas como Arranjo, ou seja, tirar a bola B1, B2 ou B2, B1. Da mesma forma para as amarelas.
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 13:46
por alexandre32100 » Sex Nov 19, 2010 13:46
O que importa neste caso são quais bolas você vai por na segunda urna, "a ordem não importa", portanto temos uma combinação.
-
alexandre32100
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- n urnas, x bolas brancas e y bolas pretas...Qstão interessan
por marcosmuscul » Seg Out 28, 2013 17:40
- 0 Respostas
- 1525 Exibições
- Última mensagem por marcosmuscul

Seg Out 28, 2013 17:40
Estatística
-
- Probabilidade - Bolas pretas e brancas
por gustavowelp » Sáb Jun 26, 2010 11:08
- 1 Respostas
- 1446 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 26, 2010 11:42
Estatística
-
- Probabilidade - Bolas
por Cleyson007 » Qui Set 22, 2011 12:23
- 3 Respostas
- 2379 Exibições
- Última mensagem por Neperiano

Qui Set 22, 2011 16:21
Estatística
-
- [Probabilidade] Bolas
por Lidstew » Qua Abr 10, 2013 21:40
- 1 Respostas
- 1801 Exibições
- Última mensagem por Rafael16

Qua Abr 10, 2013 22:19
Probabilidade
-
- Análise Combinatória - Bolas em caixas
por angeruzzi » Dom Mai 16, 2010 01:33
- 5 Respostas
- 7614 Exibições
- Última mensagem por Douglasm

Ter Jun 08, 2010 09:33
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


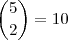 maneiras.
maneiras.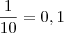
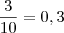

 é resultado da escolha de duas bolas dentre as três amarelas existentes na urna,
é resultado da escolha de duas bolas dentre as três amarelas existentes na urna, 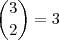 .
. , assim temos uma probabilidade de
, assim temos uma probabilidade de 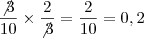 .
. na segunda, ou ainda,
na segunda, ou ainda,  .
.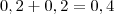 .
.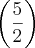 ...
... , mas isto é o mesmo que
, mas isto é o mesmo que  ou
ou  .
. , diferente do caso das bolas amarelas (
, diferente do caso das bolas amarelas ( ,
,  e
e 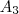 ), onde eu posso formar três pares:
), onde eu posso formar três pares:  .
.