 por Roberta » Sáb Jun 28, 2008 12:36
por Roberta » Sáb Jun 28, 2008 12:36
Olá Pessoal !!

Questões simples mas não estou chegando ao resultado correto.

Obrigada!

(1) Quantas são as palavras de 4 letras, formadas apenas por vogais, que têm exatamente duas letras iguais?
(a) 60 / (b) 120 / (c) 130 / (d) 240 / (e) 360
Pq e) 360 e não a) 60 ??

(2) Uma placa de um carro brasileira é uma seqüência de três letras seguidas de quatros algarismos (LETRA LETRA LETRA – ALGARISMO ALGARISMO ALGARISMO ALGARISMO). Dispõe-se 26 letras distintas e dez algarismos distintos para a confecção das placas. Quantas placas podem ser confeccionadas de modo que comece sempre com B e R nessa ordem?
Minha resposta foi
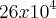
, mas a resposta correta é
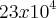
.
Não entendi pq 23 e não 26, já que não há menção de exclusão, não repetição ou algo assim.

Obrigada e bom fim de semana pra vcs!

Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
 por Roberta » Sáb Jun 28, 2008 15:58
por Roberta » Sáb Jun 28, 2008 15:58
ih... pessoal, retificando .... aí em cima ... na f'órmula ... onde aparece xis é sinal de multiplicação, okay?


MAIS UM EXERCÍCIO...

17) (PUC-Campinas) Usando os algarismos 2, 3, 4, 5, 6, 8 e 9, pergunta-se:
a) quantos nrs distintos de 3 algarismos podemos formar?
b) quantos nrs de 3 algarismos distintos podemos formar?
c) quantos nrs de 3 algarismos distintos, pares podemos formar?
d) quantos nrs de 3 algarismos distintos, pares e maiores que 234 podemos formar?
Este aqui... fui bem até letra C...
na D... cada vez que eu tentava, a resposta mudava...



Já comi 2 caixas de BIS azul pensando em como resolver esta questão!! rsss
MInhas respostas:
a)

= 343
b) 7x6x5 = 210
c) IPP+IIP+PIP+PPP= 120
d) 117 ou deveria ser 120-1= 119 ?
Por que dá diferença de 3 nrs (120-117=3) ??
Ai, vou comer outra caixa de BIS...rssrs...
Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
 por Molina » Sáb Jun 28, 2008 17:42
por Molina » Sáb Jun 28, 2008 17:42
Roberta escreveu:17) (PUC-Campinas) Usando os algarismos 2, 3, 4, 5, 6, 8 e 9, pergunta-se:
a) quantos nrs distintos de 3 algarismos podemos formar?
b) quantos nrs de 3 algarismos distintos podemos formar?
c) quantos nrs de 3 algarismos distintos, pares podemos formar?
d) quantos nrs de 3 algarismos distintos, pares e maiores que 234 podemos formar?
Este aqui... fui bem até letra C...
na D... cada vez que eu tentava, a resposta mudava...


MInhas respostas:
a)

= 343
b) 7x6x5 = 210
c) IPP+IIP+PIP+PPP= 120
d) 117 ou deveria ser 120-1= 119 ?
Por que dá diferença de 3 nrs (120-117=3) ??
Boa tarde, Roberta.
Na letra D, 3 algarismos distintos, pares totalizam 120 (como você tinha feito), porém, há uma outra condição: maiores que 234. Se você perceber, apenas um número menor ou igual a 234 será formado, ou seja, o próprio 234. Todos os outros
119 são maiores do que 234.
Sua resposta tinha dado 117?
Quais os outros algarismos que voce considerou menor que 234?
Bom estudo!
E bom bis tambem!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sáb Jun 28, 2008 18:26
por Molina » Sáb Jun 28, 2008 18:26
Roberta escreveu:(1) Quantas são as palavras de 4 letras, formadas apenas por vogais, que têm exatamente duas letras iguais?
(a) 60 / (b) 120 / (c) 130 / (d) 240 / (e) 360
Pq e) 360 e não a) 60 ??

Olá Roberta.
Primeiramente quero dizer que a princípio eu tambem colocaria a resposta como 60, ja que 60 = 5 * 1 * 4 * 3
Porém, tava analisando as palavras e verifiquei que essas duas letras que são iguais, podem e devem tomar posições diferentes. É um tanto dificil de explicar, imagino de entender, mas vou tentar ser o mais claro possível:
Formação das palavras:
- duas vogais iguais e outras duas diferentes (entre si):
AAEI
AAEO
AAEU
-
AAIE
AAIO
AAIU
-
AAOE
AAOI
AAOU
-
AAUE
AAUI
AAUO
Ou seja, com a letra A repetindo duas vezes conseguimos 12 palavras. Logo, sao 5 vogais, temos 12 * 5 = 60
Ok, provavelmente foi até ai que a Srita. chegou.
Agora temos que perceber que as vogais iguais nao necessariamente precisam ficar juntas. Temos as seguintes variantes:
1)
A A _ _
2) _ _
A A3)
A _
A _
4)
A _ _
A5)
A _ _
A6) _
A _
AComo isso vai acontecer com todas as 60 palavras formas até agora, multiplicamos por 6.
Logo temos 60 * 6 = 360

Garanto que esse nao é o melhor método de resolver essa questão. Provavelmente usando Combinatória e permutação juntas você chega no valor de forma mais simples. Porém, nao consegui assimilar por esse caminho.
Espero ter ajudado do que confundido mais.
Até a próxima!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Roberta » Sáb Jun 28, 2008 18:37
por Roberta » Sáb Jun 28, 2008 18:37
OI Molina!
Boa Tarde!
Obrigada pelas respostas!!
Sobre a dúvida (1) palavras de 4 letras... realmente... deixei de contar as mudanças de lugar das letras repetidas. Seria o correspondente a 2! É por isso que não dava certo! rss
Sobre a dúvida (3) ... foi isso mesmo! Ao invés de eliminar 1 a 1 os nrs. inferiores a 234 (que é apenas o próprio 234) eu eliminei o 4 da combinação 2 I P ... por isso ficaram faltando 2 elementos no resultado!!
Meu post ficou meio truncado... Tem mais uma dúvida que eu acho que ficou perdida ... e acabou sem resposta... se puder... Placas de carro... transcrita abaixo:
(2) Uma placa de um carro brasileira é uma seqüência de três letras seguidas de quatros algarismos (LETRA LETRA LETRA – ALGARISMO ALGARISMO ALGARISMO ALGARISMO). Dispõe-se 26 letras distintas e dez algarismos distintos para a confecção das placas. Quantas placas podem ser confeccionadas de modo que comece sempre com B e R nessa ordem?
Minha resposta foi, mas a resposta correta é .
Não entendi pq 23 e não 26, já que não há menção de exclusão, não repetição ou algo assim
Vlw Molina!!

Mais uma vez obrigada pela resposta

Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
 por Roberta » Sáb Jun 28, 2008 18:42
por Roberta » Sáb Jun 28, 2008 18:42
Ih... ó a falta que a edição faz...

Mas o Fabio vai ver isso né? legal!

Faltou este aqui!!
(2) Uma placa de um carro brasileira é uma seqüência de três letras seguidas de quatros algarismos (LETRA LETRA LETRA – ALGARISMO ALGARISMO ALGARISMO ALGARISMO). Dispõe-se 26 letras distintas e dez algarismos distintos para a confecção das placas. Quantas placas podem ser confeccionadas de modo que comece sempre com B e R nessa ordem?
Minha resposta foi

, mas a resposta correta é

.
Não entendi pq
23 e não
26, já que não há menção de exclusão, não repetição ou algo assim.
Obrigada!

Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Análise Comb.
por RJ1572 » Qua Mai 19, 2010 12:12
- 1 Respostas
- 1668 Exibições
- Última mensagem por MarceloFantini

Qua Mai 19, 2010 15:09
Estatística
-
- análise comb com cargos
por adrianosaldanha » Qui Out 20, 2011 17:03
- 1 Respostas
- 1432 Exibições
- Última mensagem por Neperiano

Qui Out 20, 2011 17:14
Sequências
-
- Questão prova concurso (análise comb.)
por fernandocez » Qui Mar 24, 2011 10:20
- 6 Respostas
- 4801 Exibições
- Última mensagem por fernandocez

Qui Mar 24, 2011 12:23
Estatística
-
- Dúvida de Prob.
por RJ1572 » Seg Mai 24, 2010 11:20
- 1 Respostas
- 1493 Exibições
- Última mensagem por Lucio Carvalho

Seg Mai 24, 2010 15:58
Estatística
-
- Dúvida prob. de Estatística
por RJ1572 » Dom Jan 23, 2011 22:07
- 1 Respostas
- 2705 Exibições
- Última mensagem por RJ1572

Ter Fev 08, 2011 15:51
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
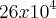 , mas a resposta correta é
, mas a resposta correta é 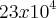 .
. 

 = 343
= 343
 , mas a resposta correta é
, mas a resposta correta é  .
. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: