Uma máquina de enchimento automático de garrafas está regulada de tal forma que a quantidade (em centilitros) de vinho vertido para uma garrafa é uma variável aleatória X com distribuição aproximadamente normal de valor médio 78.
O departamento de controlo de qualidade da empresa verificou que, em média, 15,865% das garrafas enchidas pela máquina tinham menos do que os 75 centilitros de vinho indicados no rótulo.
a)Qual é o desvio padrão da variável aleatória X ?
b)Em nome da sua boa imagem, a empresa quer diminuir drasticamente a percentagem de garrafas com menos de 75 centilitros de vinho. A regulação da máquina de enchimento permite modificar o valor médio da variável aleatória X , mas não permite alterar o seu desvio padrão. Para que novo valor médio deverá ser a máquina regulada, de tal forma que apenas 2,275% das garrafas fiquem com menos de 75 centilitros de vinho?


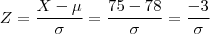
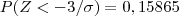
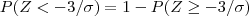 temos que
temos que 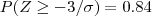
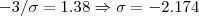
 .
. é fixado, então cabe achar o valor de
é fixado, então cabe achar o valor de  para a probabilidade solicitada.
para a probabilidade solicitada.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
