





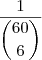 , assim, fazendo
, assim, fazendo 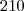 jogos distintos, as chances aumentam para
jogos distintos, as chances aumentam para 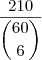 .
.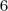 números dentre os
números dentre os  escolhidos como
escolhidos como 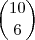 , assim suas chances são de
, assim suas chances são de 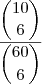 .
.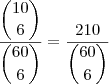 , independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de
, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de  reais.
reais. 

alexandre32100 escreveu:Num jogo normal, a sua chance é de, assim, fazendo
jogos distintos, as chances aumentam para
.
Agora, fazendo um jogo de dez números, podemos contar qualquer combinação denúmeros dentre os
escolhidos como
, assim suas chances são de
.
O engraçado é que, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de
reais.
Espero ter sido útil.
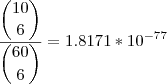
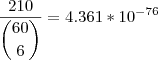

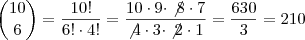
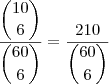 .
.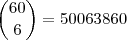
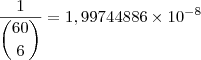
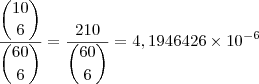
alexandre32100 escreveu:Rogério,
pode depender do método que você utilizou para calcular a divisão ou o binômio, mas acompanhe meus cálculos:
Por afirmei que.
Se quiser usar uma representação decimal:
E também
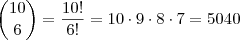
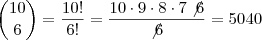
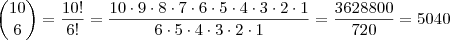

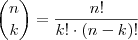 , por isso da diferença entre as soluções.
, por isso da diferença entre as soluções.felipecchaves escreveu:Acho que esse não é o lugar certo pra essa pergunta, mas vou aproveitar o tópico.
Por exemplo:
Se eu pegar 9 números e fizer todas as combinações possíveis da um total de 84 jogos e o valor da aposta é de R$ 168,00. O que é o mesmo que eu jogar 9 números na mesma cartela.
No caso de eu jogar 9 números na mesma cartela, se eu ganhar uma quadra, por exemplo, eu recebo proporcional ou recebo apenas como um jogo?
Caso o valor do premio seja proporcional é melhor jogar os 9 na mesma cartela, porque nas 84 combinações possíveis nem todas terão uma quadra. Eu to certo nisso?
 apostas separadamente.
apostas separadamente. 
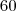 números numa só cartela. Pelo que já foi visto nesse tópico, o preço seria de
números numa só cartela. Pelo que já foi visto nesse tópico, o preço seria de 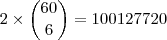 reais. Fica a dica: da próxima vez que a Mega Sena acumulada ultrapassar este valor, aposte e torça para ganhar o prêmio sozinho.
reais. Fica a dica: da próxima vez que a Mega Sena acumulada ultrapassar este valor, aposte e torça para ganhar o prêmio sozinho. 






Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.