Fatorial de 0

por **Neperiano** » Qua Set 14, 2011 19:45

Ola

Pessoal isso foi uma duvida de um colega meu de aula, mas a professora não soube tambem, então quero ver quem mata essa

Porque o fatorial de 0 é 1

Não basta dizer a porque foi convencionado assim ou explicações de lógica, quero saber através de calculos matemáticos, ou seja

Prove que fatorial de 0 é 1

Atenciosamente

por **MarceloFantini** » Qua Set 14, 2011 20:27

Isso é uma definição, não pode ser provado.

por **Neperiano** » Qui Set 15, 2011 11:33

Ola

Era bem isso que eu não queria ouvir

Desculpe marcelofantini, mas nada na natureza não pode ser provado, tu não pode dizer isso, porque se isso é uma definição como aplica-la, tenque ter alguma explicação, o fato dessa resposta é que você tambem não sabe, xd

Ja ouvi respostas do tipo, ah pense que tem 5 pessoas numa fila, quantas maneiras de organizar a fila 5!, e se tem 0 pessoas, tem 1 maneira de organizar a fila, ou seja sem ninguem, mas tenque haver uma definição sim

Atenciosamente

por **MarceloFantini** » Qui Set 15, 2011 17:03

Primeiramente, seria interessante que você leia este artigo que fala dos teoremas da incompletude de Godel, que diz que num sistema de axiomas consistente existem afirmações que são verdadeiras mas não podem ser provadas, ou seja, o sistema não é completo. Da mesma forma, se um sistema é completo existe alguma inconsistência nele, há algum problema em algum lugar. Isso desmente que "nada na natureza não pode ser provado".

Sobre a definição, é bem simples. Vou pegar outro exemplo, porque dizemos que quando uma combinação linear de vetores $a_1x_1 + a_2x_2 + \cdots + a_nx_n =0$ é linearmente independente se todos os a_i = 0

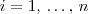, para $i=1, \, \ldots, \, n$ ? Resposta: pois isto é uma definição. Aliás, nisto mesmo já estamos usando outra definição: o que é uma combinação linear de vetores? Resposta: $a_1x_1 + a_2x_2 + \cdots + a_nx_n$ . Porque é assim? Resposta: porque é uma definição. Definições são feitas por várias razões. Primeira: é conveniente. Segunda: costuma-se definir a mais natural e prática.

A definição de que 0!=1

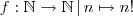é conveniente em vários aspectos: primeiro, isto mantém a definição de fatorial como uma função que leva em um número inteiro; segundo, é um número simples de se trabalhar, não altera o produto; terceiro, com isso incluímos no fatorial o caso em que o zero aparece. Da mesma forma que um fatorial é definido como uma função $f: \mathbb{N} \to \mathbb{N} \, | \, n \mapsto n!$ , com essa definição nós estendemos a função para quando n=0

(que nem sempre é incluído nos naturais).

por **Claudin** » Qui Set 15, 2011 17:48

Em relação a mensagem abaixo:
Correto, então resumindo, as demonstrações de definição o aluno tem que "aceitar" e o que pode ser provado são as propriedades e as fórmulas.
Desculpe-me pelo equívoco.

por **MarceloFantini** » Qui Set 15, 2011 17:52

Está equivocado, pois definição não se demonstra, aceita-se e procura-se compreender o significado e as razões por trás dela.

por **LuizAquino** » Qui Set 15, 2011 18:51

Olá Pessoal,

Primeiro, vamos esclarecer alguns conceitos. Como o colega Fantini lembrou, não provamos definições.

Vejamos um exemplo. Uma circunferência é definida como "o conjunto de todos os pontos do plano que são equidistantes de um ponto fixo (chamado de centro)".

Já que isso é a definição de circunferência, não faz sentido dizermos: "Prove que a circunferência é o conjunto de todos pontos do plano que são equidistantes de um ponto fixo (chamado de centro)".

Esclarecido essa parte, vejamos agora a questão particular de dizer que 0! tem valor igual a 1.

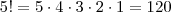Como bem sabemos, nós definimos o fatorial do número inteiro (positivo) n, como sendo o produto entre todos os inteiros de 1 até n. Nós representamos essa operação por n!. Ou seja, colocamos o símbolo de exclamação ("!") ao lado do número. Como exemplo, temos que $5! = 5\cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$ . Em particular, notamos também que 1! = 1.

Manipulando agora a definição de fatorial, podemos escrever que n(n-1)! = n!. Vale destacar que no primeiro membro o fatorial está aplicado apenas no número (n-1) e não mais no número n.

Vamos analisar o que acontece com essa identidade quando n = 1. Nesse caso ficamos com 1(1 - 1)! = 1!. Nós já sabíamos que 1! = 1. Além disso, se multiplicamos 1 pelo número (1 - 1)!, então temos como resultado o próprio número (1 - 1)!. Isso significa que podemos escrever (1 - 1)! = 1. Lembrando que nós partimos apenas da definição de fatorial, para que essa definição seja condizente precisamos então ter que 0! = 1.

Por outro lado, infelizmente notamos que 0! não pode ser calculado diretamente da definição de fatorial, pois o produto entre todos os inteiros de 1 até 0 é zero. Dessa maneria, a argumentação acima serve apenas para ilustrar a necessidade de atribuirmos 1 ao valor de 0!, pois caso contrário a definição de fatorial não seria condizente. Isso porque se 0! tivesse outro valor diferente de 1, digamos c, então da identidade n(n-1)! = n! chegaríamos que 1! = c, mas sabemos que 1! é 1 e portanto não podemos ter 1! = c.

A partir disso, precisamos então definir que 0! = 1.

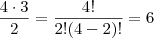Deixando as argumentações um pouco mais intuitivas. Vamos analisar que a necessidade de termos 0! = 1 é razoável. Considere que em um grupo de 4 pessoas, cada uma deva apertar a mão das outras apenas uma vez. Teremos ao todo $\frac{4 \cdot 3}{2} = \frac{4!}{2!(4-2)!} = 6$ apertos de mão distintos. De modo geral, se temos n pessoas teremos $\frac{n!}{2!(n-2)!}$ apertos de mão distintos.

Agora imagine que há apenas 2 pessoas. Claramente teremos apenas 1 aperto de mão. Ou seja, precisamos ter $1 = \frac{2!}{2!(2-2)!}$ . Ou ainda, podemos escrever que devemos ter $1 = \frac{1}{0!}$ . O único valor para o número 0! que torna essa equação válida é 1. Mais uma vez percebemos a necessidade de termos definido que 0! = 1.

por **Neperiano** » Qui Set 15, 2011 19:16

Ola

Essa resposta do luizaquino ja explica um pouco melhor, se não tem como provar, como chegaram a essa definição, e sempre há um motivo para isso

É um belo trabalho de conclusão esse tema

Atenciosamente

por **LuizAquino** » Qui Set 15, 2011 20:54

Neperiano escreveu:É um belo trabalho de conclusão esse tema

Bem, com certeza é um tema curioso. Mas render um trabalho de conclusão de curso eu acho um pouco improvável.

por **Neperiano** » Sex Set 16, 2011 15:18

Ola

Olha o que um colega meu fez quando perguntei pra ele isso

n = n!/(n-1)
1=1!/0
0=1!/1
1!=0

Ele conseguiu provar desse jeito, claro que se tu usa 0 no n vai dar 0=-1, ou seja isso não vale pra tudo

Atenciosamente

por **MarceloFantini** » Sex Set 16, 2011 15:22

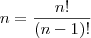Você quis dizer $n = \frac{n!}{(n-1)!}$ , mas para isso 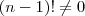$(n-1)! \neq 0$ , e se você não sabe o valor de

esse resultado é inválido para n=1. Já que você até agora não acreditou que isto é uma definição, então use que a função fatorial generalizada é a função gama:

$\Gamma (x) = \int_0^{\infty} t^{x-1} e^{-t} \, \textrm{d}t$

Quando x=0

temos $\Gamma(0) = 1$ .

por **Neperiano** » Sex Set 16, 2011 15:30

Ola

Não não

Não tem o fatorial embaixo marcelo

Mas como disse isso foi uma maneira qualquer, o objetivo era provar, e não ser lógico

Atenciosamente

por **LuizAquino** » Sex Set 16, 2011 15:33

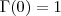Neperiano escreveu:Olha o que um colega meu fez quando perguntei pra ele isso

n = n!/(n-1)

Você deve querer dizer n = n!/(n-1)!. Isso é obtido da própria definição de n!. É apenas uma outra forma de ver a identidade n(n-1)! = n! que indiquei anteriormente. Basta dividir toda a equação por (n-1)! e teremos n = n!/(n-1)!.

MarceloFantini escreveu:Você quis dizer $n = \frac{n!}{(n-1)!}$ , mas para isso $(n-1)! \neq 0$ , e se você não sabe o valor de 0! esse resultado é inválido para n=1

Veja que não há inconsistência. Para n = 1, temos que (n-1)! é o mesmo que 0!, que por enquanto é um número que desconhecemos. Não necessariamente ele é zero, e portanto a divisão pode estar bem definida. A ideia por traz da argumentação é que conhecemos o valor de 1!, que é 1. Sendo assim, a equação fica algo do tipo $1 = \frac{1}{0!}$ . Ora, mas para essa equação ser válida só há um número que podemos atribuir para 0!, que é 1. Ou seja, precisamos ter (definir) 0! = 1.

Neperiano escreveu:Ele conseguiu provar desse jeito

Apenas frisando, isso não é uma prova de que 0! = 1. Assim como as argumentações que indiquei antes, isso serve apenas para ilustrar a necessidade de atribuirmos 1 ao valor de 0!, ou seja, a necessidade de definirmos que 0! = 1. Lembre-se sempre que esse resultado não pode ser obtido diretamente da definição de fatorial.

Como argumentei na mensagem anterior, a definição de que 0! = 1 surge da necessidade de deixar a própria definição de fatorial condizente.

por **Neperiano** » Sex Set 16, 2011 15:38

Ola

Novamente, não é Fatorial embaixo, pode ser que a definição seja isso, mas ele não colocou ela embaixo, porque olha o que eu fiz antes

Neperiano escreveu:Ola

Olha o que um colega meu fez quando perguntei pra ele isso

n = n!/(n-1)
1=1!/0
0=1!/1
1!=0

Ele conseguiu provar desse jeito, claro que se tu usa 0 no n vai dar 0=-1, ou seja isso não vale pra tudo

Atenciosamente

Não tem o fatorial embaixo, é assim que ele fez

E eu não falei que estava certo ou errado, só disse que ele fez assim

Atencisosamente

por **LuizAquino** » Sex Set 16, 2011 15:42

Neperiano escreveu:(...) Novamente, não é Fatorial embaixo, pode ser que a definição seja isso, mas ele não colocou ela embaixo (...)

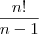Se ele não colocou o símbolo de fatorial, então a argumentação dele está inválida. Note que o valor de $\frac{n!}{n-1}$ seria diferente de n. Faça um teste. Escolha, por exemplo, n = 4 e faça os cálculos.

por **MarceloFantini** » Sex Set 16, 2011 15:45

Então vamos esclarecer alguns fatos sobre a tentativa de seu amigo: primeiro, ele não provou nada; segundo, a relação está errada, pois tome n=5

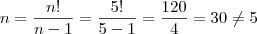, teremos $n = \frac{n!}{n-1} = \frac{5!}{5-1} = \frac{120}{4} = 30 \neq 5$ . E novamente você não conseguirá provar pois isto é uma definição, e qualquer tentativa será na verdade apenas uma motivação para a definição.

por **Neperiano** » Sex Set 16, 2011 15:48

Ola

Mas o que eu falei, eu disse que só dava para 0, quanto ao fatorial embaixo, eu coloquei errado ali antes

Era pra ter embaixo sim

Ficaria

n = n!/(n-1)!
1=1!/0!
0!=1

Mas que seja, só disse que deu assim, não falei que tava certo

Tomara que agora esse topico pare