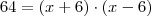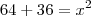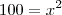Eu sei ate resolver equação do 2º grau usando o delta e Baskara, mas tenho um indice muito grande em resolver problemas como esse "A área de um retângulo é de 64cm quadrado . Nessas condições, determine as dimensões do retângulo sabendo que o comprimento mede (x+6) m e a largura mede (x- 6) m.". A minha dificuldade esta em montar a equação para resolver.
Se alguem souber a onde posso encontrar alguns problemas que ensine fazer as formulas, me indique pra que posso praticar;
Desde ja estou agradecido.


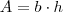 , onde
, onde