 por zig » Qua Jul 20, 2011 17:25
por zig » Qua Jul 20, 2011 17:25
em uma cesta tinha uma certa quantidade de ovos, as galinhas do meu quintal botaram 10% da quantia de ovos que eu tinha na cesta e nela eu os coloquei.
mas por um azar meu, um objeto caiu sobre a cesta e 10% dos ovos foram quebrados, eu tenho mais ovos agora ou inicialmente?
-
zig
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Sex Fev 18, 2011 18:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Jul 20, 2011 17:41
por MarceloFantini » Qua Jul 20, 2011 17:41
Você tinha inicialmente N ovos. Com os novos ovos, ficou com
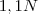
. Depois da queda do objeto, perdeu 10%, ou seja,

, portanto havia mais ovos inicialmente. Acredito que a resolução seja assim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Jul 20, 2011 17:44
por Claudin » Qua Jul 20, 2011 17:44
zig escreveu:em uma cesta tinha uma certa quantidade de ovos, as galinhas do meu quintal botaram 10% da quantia de ovos que eu tinha na cesta e nela eu os coloquei.
mas por um azar meu, um objeto caiu sobre a cesta e 10% dos ovos foram quebrados, eu tenho mais ovos agora ou inicialmente?
Para facilitar sua vida Zig, substitua em valores como por exemplo:
Suponha que tenha colocado inicialmente na cesta 100 ovos. No entanto, as galinhas botaram 10% da quantia que havia na cesta, ou seja, 10% de 100 seria mais 10 ovos, totalizando 110 ovos na cesta. Porém, 10% do total que estava na cesta foi quebrado, ou seja, 10% de 110 que seria 11. Concluindo se 10% de 110 é igual a 11, e a quantia inicial da cesta era 100, conclui-se que a cesta iria ter menos ovos do que inicialmente, que seriam exatamente

ovos.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jul 20, 2011 17:46
por Claudin » Qua Jul 20, 2011 17:46
Não tinha visto o post de Marcelo Fantini, eu fiz de um modo mais prático, mas o Fantini fez do modo mais correto. Sempre o melhor lado é escolher pela teoria como Marcelo Fantini optou, porém, percebi que você não dominava tal área e preferi utilizar a casualidade, substituindo por 100 no valor, sempre fica mais fácil o compreendimento de exercícios de porcentagem.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4571 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7886 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3743 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3668 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2909 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


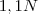 . Depois da queda do objeto, perdeu 10%, ou seja,
. Depois da queda do objeto, perdeu 10%, ou seja,  , portanto havia mais ovos inicialmente. Acredito que a resolução seja assim.
, portanto havia mais ovos inicialmente. Acredito que a resolução seja assim.

 ovos.
ovos.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.