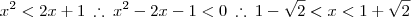por Questioner » Dom Mai 16, 2010 17:13
por Questioner » Dom Mai 16, 2010 17:13
Olá,
Estou com uma dificuldade na seguinte desigualdade (muito tempo sem fazer exercícios dessa forma). Será que dá para dar uma luz?

Eu consegui fazer algumas divisões e cheguei em:

Gabarito é:

e
![1+ \sqrt[]{2} 1+ \sqrt[]{2}](/latexrender/pictures/a1e50b8675f5d91bf143fae9923d5966.png)
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglasm » Dom Mai 16, 2010 18:37
por Douglasm » Dom Mai 16, 2010 18:37
Façamos novamente por partes:
1ª condição:

(Isso pode ser facilmente notado pelo gráfico da função. Como a concavidade desta é voltada para cima, os valores maiores que zero serão aqueles que
não estarão entre as raízes.)
2ª condição:
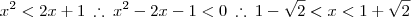
(Aqui os valores da função menores que zero estarão entre as raízes.)
Unindo as duas condições:

Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desigualdade
por Claudin » Qui Jan 17, 2013 14:50
- 2 Respostas
- 2558 Exibições
- Última mensagem por Claudin

Sex Jan 18, 2013 20:14
Álgebra Linear
-
- Resolvendo a desigualdade...
 por Aliocha Karamazov » Qua Abr 06, 2011 19:55
por Aliocha Karamazov » Qua Abr 06, 2011 19:55
- 3 Respostas
- 2580 Exibições
- Última mensagem por Aliocha Karamazov

Qua Abr 06, 2011 23:20
Funções
-
- integral com a desigualdade
por stuart clark » Seg Mai 30, 2011 00:36
- 1 Respostas
- 1622 Exibições
- Última mensagem por Neperiano

Qua Jun 22, 2011 09:54
Cálculo: Limites, Derivadas e Integrais
-
- Desigualdade Triangular
por Claudin » Sex Set 09, 2011 09:40
- 1 Respostas
- 1872 Exibições
- Última mensagem por LuizAquino

Sex Set 09, 2011 10:56
Cálculo: Limites, Derivadas e Integrais
-
- desigualdade:prova
por Victor Gabriel » Ter Jun 18, 2013 13:48
- 0 Respostas
- 1102 Exibições
- Última mensagem por Victor Gabriel

Ter Jun 18, 2013 13:48
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e ![1+ \sqrt[]{2} 1+ \sqrt[]{2}](/latexrender/pictures/a1e50b8675f5d91bf143fae9923d5966.png)



 e
e ![1+ \sqrt[]{2} 1+ \sqrt[]{2}](/latexrender/pictures/a1e50b8675f5d91bf143fae9923d5966.png)