Olá, pessoal!
Um distribuidor comercializa três tipos de farinha (I, II e III), obtidas por meio de misturas em proporções diferentes de três tipos de grãos (A, B e C).
A tabela mostra as quantidades em gramas de cada tipo de grão (A, B, C) na fabricação de pacotes de 500 gramas de cada tipo de farinha (I, II, III).
Esse distribuidor possui um estoque de 50 KG de grãos do tipo A, 26 Kg de grãos do tipo B e 24 Kg de grãos do tipo C e vai utilizar todo o material para produzir os três tipos de farinha.
Qual o número de pacotes de 500 g de farinha do tipo III que ele produzirá?
A resposta é 60 pacotes.
Tentei montar um sistema, sabendo que, no total, ele deve produzir 200 pacotes de farinha, mas não consegui estabelecer a quantidade exata a ser produzida de cada tipo de farinha, de modo a utilizar toda a matéria-prima, respeitando a proporcionalidade das misturas....
Aguardo, grato.



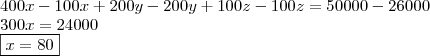

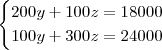



 , avisa que eu resolvo.
, avisa que eu resolvo.

