 por roberto Marinho » Sex Out 16, 2009 04:38
por roberto Marinho » Sex Out 16, 2009 04:38
olá, não sei se esse é lugar certo para esse tipo de pergunta , mais espero que me ajude , por favor tem um questão que está tirando o meu sono.
A QUESTÃO É ASSIM: EM UM COFRE TINHAM 512 MOEDAS, DE 0,50 E DE 1,OO QUE TOTALIZAVAM 423,00.QUANTAS MOEDAS DE CINCOENTA HAVIAM NO COFRE?
EU JÁ DIVIDI 512 POR CINCOENTA E NÃO CHEGUEI NO RESULTADO,JÁ DIVIDI 423 POR CINCOENTA E NÃO CHEGUEI NO RESULTADO,MAIS SEI QUE É 178 SEI TAMBÉM QUE TEM UMA MANEIRA DE SE CHEGAR NO RESULTADO DE RÁPIDA E PRECISA.PODE ME AJUDAR.Obrigado.
-
roberto Marinho
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 16, 2009 03:55
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por admin » Sex Out 16, 2009 05:03
por admin » Sex Out 16, 2009 05:03
Olá Roberto, boas-vindas!
Seu tópico foi movido para uma seção mais apropriada, já é uma dica.

Em outras palavras, você pode resolver o problema montando um sistema com duas equações extraídas do enunciado.
Se nomearmos de

: a quantidade de moedas de cinquenta;

: a quantidade de moedas de um;
Esta já é a primeira equação, veja:

Escreva a outra a partir do enunciado e resolva o sistema por substituição, assim encontrará o valor para

.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Sex Out 16, 2009 14:16
por Cleyson007 » Sex Out 16, 2009 14:16
fabiosousa escreveu:Olá Roberto, boas-vindas!
Seu tópico foi movido para uma seção mais apropriada, já é uma dica.

Em outras palavras, você pode resolver o problema montando um sistema com duas equações extraídas do enunciado.
Se nomearmos de

: a quantidade de moedas de cinquenta;

: a quantidade de moedas de um;
Esta já é a primeira equação, veja:

Escreva a outra a partir do enunciado e resolva o sistema por substituição, assim encontrará o valor para

.
Até mais!
Olá boa tarde!
Meu amigo Fabio Sousa, que bom tê-lo participando do fórum novamente!
Quanto ao exercício:
Roberto, assim com o Fabio disse, você precisa encontrar a outra equação..
--> O problema trabalha com duas situações: 1ª) Quantidade de moedas.
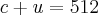
2ª) Valor que tem no cofre.
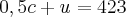
Daí, resolva o sistema por substituição.
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Seg Out 19, 2009 14:10
por Molina » Seg Out 19, 2009 14:10
Só para contribuir com outra forma de solução, dá para subtrair uma equação pela outra.
Note que em ambas tem

, fazendo a subtração este

vai "sumir" e ficamos apenas com a variável


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Moedas
 por admin » Sex Jul 20, 2007 15:08
por admin » Sex Jul 20, 2007 15:08
- 13 Respostas
- 9813 Exibições
- Última mensagem por Neperiano

Qua Out 29, 2008 20:59
Desafios Fáceis
-
- Moedas
por andersonsouza » Seg Fev 11, 2013 16:16
- 3 Respostas
- 2064 Exibições
- Última mensagem por young_jedi

Ter Fev 12, 2013 11:15
Aritmética
-
- problema das moedas
 por marquessbr » Qua Abr 04, 2012 22:04
por marquessbr » Qua Abr 04, 2012 22:04
- 2 Respostas
- 2180 Exibições
- Última mensagem por marquessbr

Qui Abr 05, 2012 09:19
Estatística
-
- [Lançamento de moedas] Probabilidade
por analuzia » Qua Nov 07, 2012 16:33
- 2 Respostas
- 2896 Exibições
- Última mensagem por analuzia

Qua Nov 07, 2012 17:04
Probabilidade
-
- [Probabilidade de esferas] condicionadas com moedas
por Thebigspire » Qua Set 24, 2014 01:31
- 1 Respostas
- 3884 Exibições
- Última mensagem por Thebigspire

Sex Out 03, 2014 00:40
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 : a quantidade de moedas de cinquenta;
: a quantidade de moedas de cinquenta; : a quantidade de moedas de um;
: a quantidade de moedas de um;

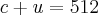
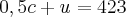




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.