


Como disse no tópico anterior, ja vi toda matéria e estou revisando algumas coisas,mas sistema eu não me lembro como se resolve.Gostaria de um ajuda nessa questão.





GABRIELA escreveu:Quero saber ql procedimento para esse sistema:
Como disse no tópico anterior, ja vi toda matéria e estou revisando algumas coisas,mas sistema eu não me lembro como se resolve.Gostaria de um ajuda nessa questão.





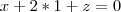
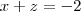
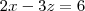

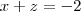
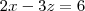


molina escreveu:GABRIELA escreveu:Quero saber ql procedimento para esse sistema:
Como disse no tópico anterior, ja vi toda matéria e estou revisando algumas coisas,mas sistema eu não me lembro como se resolve.Gostaria de um ajuda nessa questão.
Como eu informei no outro tópico, há mais de um caminho para o mesmo fim.
Então vou propor o meu:
Pegar a equação 3 e subtrair da equação 1:
-
-------------------------------
Obtemos uma nova equação:
Aplicamos este valos nas equações, obtendo:
logo:
Note que a primeira e a terceira equações ficaram iguais. Então podemos apenas considerar a primeira e a segunda, com duas variáveis:
Agora basta você fazer o procedimento feito naquela do outro tópico, ok?
Bom estudo,


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)