A primeira coisa a fazer para resolver esta inequação é reduzir ambos os membros ao mesmo denominador.
Como

, basta transformarmos o denominador do segundo membro.
Assim, temos:

Calculando o produto no segundo membro, ficamos com:

Em seguida, devemos passar todos os termos para o primeiro membro:

E calculamos esta diferença:

Como o numerador e o denominador têm um fator comum, podemos transformar esta inequação da seguinte forma:
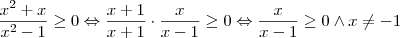
Como tanto o numerador como o denominador representam retas crescentes, a fração é positiva antes da raiz do numerador e depois da raiz do denominador. Assim, temos
![\frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \} \frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \}](/latexrender/pictures/7f53c2dd04331aa446df59ea6fa26298.png)
Espero ter ajudado. Se não perceber algum dos passos da resolução, tentarei explicar melhor.



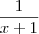 é:
é:



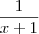 é:
é:
 , basta transformarmos o denominador do segundo membro.
, basta transformarmos o denominador do segundo membro.



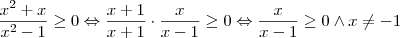
![\frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \} \frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \}](/latexrender/pictures/7f53c2dd04331aa446df59ea6fa26298.png)

