
"A solução da inequação


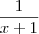 é:
é:



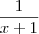 é:
é:
 , basta transformarmos o denominador do segundo membro.
, basta transformarmos o denominador do segundo membro.



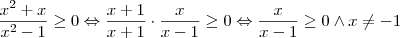
![\frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \} \frac{ x }{x-1} \geq 0 \wedge x\neq -1 \Leftrightarrow x\in \left ((-\infty ,0] \cup [1,+\infty ) \right )\setminus \left \{ -1 \right \}](/latexrender/pictures/7f53c2dd04331aa446df59ea6fa26298.png)

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

