[Sistemas de Equações] trigonométricas

por **Aliocha Karamazov** » Qui Nov 17, 2011 17:43

Pessoal, ao resolver um exercício de física, no qual preciso encontrar $\theta_{1}$ e $\theta_{2}$ , apareceu um sistema que eu não sei resolver. Na situação física, ambos os ângulos são menores que $\frac{\pi}{2}$ .

O sistema é:
$1,5\cos\theta_{1}=2\cos\theta_{2}$
$1,5\sin\theta_{1}+2\sin\theta_{2}=2,5$

Eu pensei em usar coisas como $\cos\theta_{1}=\sqrt{1-\sin^2\theta_{1}}$ , mas tenho a impressão de que essa não é a melhor maneira. Alguém pode me ajudar?

por **TheoFerraz** » Qui Nov 17, 2011 17:50

da primeira equação do seu sistema voce obtém que :

$cos {\theta}_{2} = \frac{1.5}{2} cos{\theta}_{1} = \frac{3}{4} cos{\theta}_{1}$

e como voce mesmo percebeu, temos que:

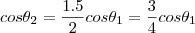
$cos {\theta}_{2}= \sqrt[]{1-sen{\theta}_{2}} = \frac{3}{4} cos{\theta}_{1}$

com isso, voce chega que:

$sen{\theta}_{2} = 1-{\left( \frac{3}{4} cos{\theta}_{1} \right)}^{2}$

se voce substituir ASSIM na segunda equação, nao vai dar em nada! esse cos de theta1 não nos ajuda... entaaaaao:

$sen{\theta}_{2} = 1-{\left( \frac{3}{4} \left(\sqrt[]{1 - sen{\theta}_{1}} \right) \right)}^{2}$

dai

$sen{\theta}_{2} = 1-{\left(\frac{3}{4} \right)}^{2} \times \left(1 - sen{\theta}_{1} \right)$

substituindo isso na segunda equação voce começa a obter resultados... continue dai

por **Aliocha Karamazov** » Qui Nov 17, 2011 18:02

TheoFerraz escreveu: $sen{\theta}_{2} = 1-{\left( \frac{3}{4} cos{\theta}_{1} \right)}^{2}$

O seno não deveria estar ao quadrado aí?

por **TheoFerraz** » Qui Nov 17, 2011 18:09

SIM SIM SIM SIM SIM

em todos os momentos que eu coloquei:

$\sqrt[]{\left(1- sen{\theta}_{k} \right)}$

era pra ter sido:

$\sqrt[]{\left(1- {sen}^{2}{\theta}_{k} \right)}$

desculpe o erro, e obrigado a correção

.

por **Aliocha Karamazov** » Qui Nov 17, 2011 18:13

Eu que agradeço pelo ajuda. Vou continuar aqui.

[Sistemas de Equações] trigonométricas

[Sistemas de Equações] trigonométricas

[Sistemas de Equações] trigonométricas

Re: [Sistemas de Equações] trigonométricas

Re: [Sistemas de Equações] trigonométricas

Re: [Sistemas de Equações] trigonométricas

Re: [Sistemas de Equações] trigonométricas

Quem está online