Não consegui resolver esse problema
1. A soma de dois números racionais é -1,8. Um deles é 9,7. Calcule o outro número.
Tentei resolver e cheguei a essa conta.

está no caminho certo? se sim, como resolver essa parte
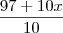 ?
?Obrigado, agradesço desde ja.


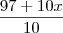 ?
?


giulioaltoe escreveu:voce nao precisa fazer o mmc entre 97/10 e x. apenas "passe" o 97/10 para o outo lado e subtraia 1,8 - 9,7 = x
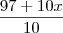 não tem nada haver né ? obrigado
não tem nada haver né ? obrigado
 . Sobre a fração: não está errada, mas é resolver a questão pelo caminho mais tortuoso. Você terá que multiplicar os dois lados por dez, depois subtrair 97 e finalmente dividir tudo por dez novamente.
. Sobre a fração: não está errada, mas é resolver a questão pelo caminho mais tortuoso. Você terá que multiplicar os dois lados por dez, depois subtrair 97 e finalmente dividir tudo por dez novamente.

MarceloFantini escreveu:Cuidado nas contas:. Sobre a fração: não está errada, mas é resolver a questão pelo caminho mais tortuoso. Você terá que multiplicar os dois lados por dez, depois subtrair 97 e finalmente dividir tudo por dez novamente.
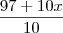 parei exatamente aqui, e nao sei continuar.
parei exatamente aqui, e nao sei continuar.

MarceloFantini escreveu:Está certo. Veja:
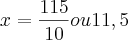



LuizCarlos escreveu:MarceloFantini escreveu:Está certo. Veja:
Ola MarceloFantini, entendi, e consegui chegar ao resultado que o livro apresenta no final que é
Só que como o amigo giulioaltoe acima explicou, tambem chega ao resultado, porem o valor de x encontrado é
diferente de
até mesmo você falou , cuidado nas contas 9,7 + x = - 1,8
x = - 1,8 - 9,7
Queria explicação sobre essa afirmação que você fez, para termos cuidado. Agradesço pela sua ajuda, voce será um otimo professor de matematica, caso queria né. Abraço




MarceloFantini escreveu:Ele esqueceu o sinal de menos no lado direito da igualdade, por isso a resposta dele está errada. Note que a minha está certa, mas no gabarito deve ter faltado o sinal de negativo, pois em valor absoluto a resposta está certa. A forma mais simples é trabalhar com os números com vírgula, só isso.
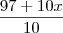 , nessa caso estou tirando o mmc, igual
, nessa caso estou tirando o mmc, igual

giulioaltoe escreveu:eu nao vi que a questao era =-1,8, pois na primeira apresentação voce pos positivo pelo latex e negativo na hora de apresentar a questao por extenso, entao nao reparei nesse detalheo metodo mais facil mesmo e fazer a conta com numeros, com virgulas!!

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

