Se alguém puder dar uma ajudinha eu agradeço!
x-2 / x+3 ? x / x+2
1º passo
(x+2)(x-2) -(x+3)x / (x+3)(x+2) ? 0
2º passo
(x²+2x-2x-4) -(x²-3x) ? 0
Minha dúvida é justamente nesse segundo passo, pois eu consigo "3x-4". No gabarito, "3x+4", não entendo onde posso ter errado. No caso 3x-4, x seria = 4/3, mas no do gabarito x = -4/3. Alguém pode me ajudar?
A formatação de formulas tá dando bronca pra mim, tive q fazer assim mesmo!


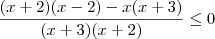

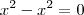 , sobra
, sobra  no numerador. Coloquei
no numerador. Coloquei  em evidência, e depois multipliquei tudo e inverti a desigualdade.
em evidência, e depois multipliquei tudo e inverti a desigualdade.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)