Por que as outras alternativas estão erradas? ALguém poderia fornecer a resolução. O gabarito é a B.
(MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a)existe AB se, e somente se, n = 4 e m = 3
b)existem AB e BA se, e somente se, n = 4 e m = 3
c)existem, iguais, AB e BA se, e somente se, A = B
d)existe A + B se, e somente se, n = 4 e m = 3
e)existem, iguais, A + B e B + A se, e somente se, A = B


 é uma matriz
é uma matriz  e
e  é uma matriz
é uma matriz 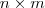 , para multiplicar você precisa ter que o número de colunas de uma seja igual ao número de linhas da outra.
, para multiplicar você precisa ter que o número de colunas de uma seja igual ao número de linhas da outra. 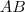 existir, você fará
existir, você fará 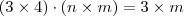 , logo
, logo  . Usei uma notação abreviada para as matrizes, mostrando apenas seus tamanhos.
. Usei uma notação abreviada para as matrizes, mostrando apenas seus tamanhos. existir você fará
existir você fará 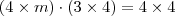 , logo
, logo 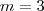 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

