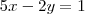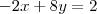por natanskt » Qua Nov 17, 2010 10:24
por natanskt » Qua Nov 17, 2010 10:24
CONSIDERE AS MATRIZES

,
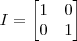
,

,
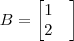
SE X E Y SÃO COLUÇOES DO SISTEMA
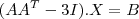
,ENTÃO X+Y É IGUAL A:
A-)2
B-)1
C-)0
D-)-1
E-)-2
QUESTÃO DIFICIL DEMAIS
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por andrefahl » Qua Nov 17, 2010 12:10
por andrefahl » Qua Nov 17, 2010 12:10
Cara essa questão não é dificil
spo envolve multiplicaçao de matrizes...
dps que vc resolver

vc subtri

multiplica esse resultado pela matriz X quando vc fizer isso vc terá uma
matriz de ordem 2x1 e ira igualar as linha dessa matriz que vc obteve
com as d B dái vc terá um sistema de duas equações com 2 icognitas...
não eh dificil eh soh num ter preguiça q nem eu d escrever tudo isso no LaTex ASASHDUASHDUAH
tenta fazer desse jeito que eu disse se vc naum conseguir eu te ajudo mais ok!
Att
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por natanskt » Qua Nov 17, 2010 16:18
por natanskt » Qua Nov 17, 2010 16:18
tentei fazer assim

.
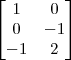
.
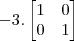
.

=
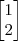
um pouco depois...
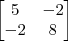
.

=

não coinsigo resolver daí,está facil mais num bate com a resposta me ajuda aew man,tenho que aprender
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por andrefahl » Qua Nov 17, 2010 16:40
por andrefahl » Qua Nov 17, 2010 16:40
Cara eu naum conferi as contas...
mas a ideia eh vc chegar em uma coisa parecida...
assim q eu tiver um tempo aki eu confiro pra vc =)
a ideia ta certa simsim
se a resp naum esta conferindo tente verificar a parte da multiplicaçao eh mto facil errar em contas nas multiplicação
d matrizes =D
Att
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7153 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3569 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6723 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4694 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4802 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
, 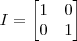 ,
, ,
,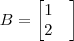 SE X E Y SÃO COLUÇOES DO SISTEMA
SE X E Y SÃO COLUÇOES DO SISTEMA 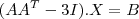 ,ENTÃO X+Y É IGUAL A:
,ENTÃO X+Y É IGUAL A:
 ,
, 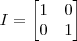 ,
, ,
,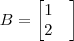 SE X E Y SÃO COLUÇOES DO SISTEMA
SE X E Y SÃO COLUÇOES DO SISTEMA 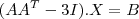 ,ENTÃO X+Y É IGUAL A:
,ENTÃO X+Y É IGUAL A:
 vc subtri
vc subtri 

 .
. 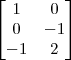 .
.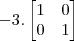 .
. =
=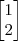
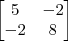 .
. =
= não coinsigo resolver daí,está facil mais num bate com a resposta me ajuda aew man,tenho que aprender
não coinsigo resolver daí,está facil mais num bate com a resposta me ajuda aew man,tenho que aprender