Cleyson007 escreveu:Considere a matriz A=
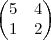
e resolva o que se pede:
a) Mostre que a matriz A é diagonalizável e determine a matriz diagonal D correspondente.
b) Determine uma matriz P tal que
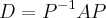
.
Cleyson007 escreveu:Bom, minha resposta não bate com o gabarito. Gostaria de saber onde estou errando:
a)
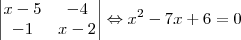
Resolvendo,
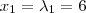
e
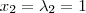
Ok. Esse são os autovalores.
Cleyson007 escreveu:Substituindo os valores de

em

, encontro:
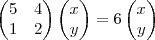
. Resolvendo, encontro:

.
Ok. Esse é um autovetor associado ao autovalor
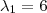
.
Cleyson007 escreveu:Agora fazendo
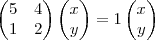
encontro:
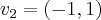
Ok. Esse é um autovetor associado ao autovalor

.
Cleyson007 escreveu:Logo, a matriz pedida é

com

. Logo, A é diagonalizável.
Ok. Mas eu presumo que você quis dizer
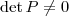
.
Cleyson007 escreveu:b)
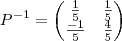
Resolvendo
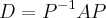
, encontro:
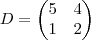
.
Está errado. Note que:

Cleyson007 escreveu:Gabarito: a)

e b)

.
Nessa resposta foi usado que

e
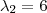
. Portanto, a primeira coluna de
P deve ser o autovetor (-1, 1). Já a segunda coluna de
P deve ser o autovetor (4, 1). Ao que parece você cometeu um erro de digitação, pois devemos ter

no gabarito.
Note que outra reposta válida é obtida quando é usado
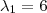
e

. Nesse caso, a primeira coluna de
P é o autovetor (4, 1). Já a segunda coluna de
P é o autovetor (-1, 1). Essa foi a resposta que você estava no caminho.
 e resolva o que se pede:
e resolva o que se pede: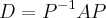 .
.
 e
e 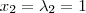
 em
em  , encontro:
, encontro: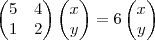 . Resolvendo, encontro:
. Resolvendo, encontro:  .
.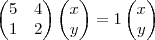 encontro:
encontro: 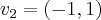
 com
com 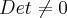 . Logo, A é diagonalizável.
. Logo, A é diagonalizável.
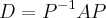 , encontro:
, encontro:  .
.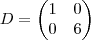 e b)
e b) 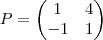 .
.


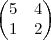 e resolva o que se pede:
e resolva o que se pede: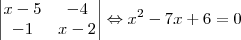
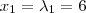 e
e 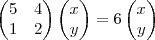 . Resolvendo, encontro:
. Resolvendo, encontro: 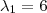 .
.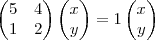 encontro:
encontro:  .
. com
com  . Logo, A é diagonalizável.
. Logo, A é diagonalizável. .
.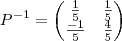
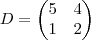 .
.
 e b)
e b)  .
. e
e 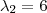 . Portanto, a primeira coluna de
. Portanto, a primeira coluna de  no gabarito.
no gabarito.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
