gabarito:
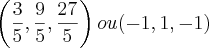

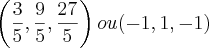

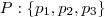 uma P.G. de três termos e
uma P.G. de três termos e  a sua razão, conforme o enunciado:
a sua razão, conforme o enunciado: 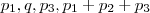 é uma P.A.
é uma P.A.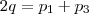 e usando a definição de progressão geométrica decorre em:
e usando a definição de progressão geométrica decorre em: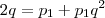 , isto é,
, isto é, 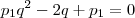 (i)
(i)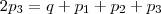 , isto é,
, isto é,  e decorre em :
e decorre em :  (ii)
(ii)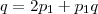 , isto é,
, isto é, 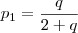 (iii) e aplicando tal relação em (i), temos:
(iii) e aplicando tal relação em (i), temos: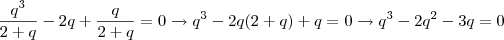 , isto é,
, isto é, 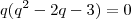
 ou
ou 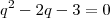 cujas raízes são
cujas raízes são 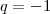 ou
ou 
 , então:
, então:  e, nesse caso, os termos da P.G. são:
e, nesse caso, os termos da P.G. são: 
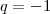 , então:
, então: 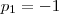 e, nesse caso, os termos da P.G. são:
e, nesse caso, os termos da P.G. são: 
 , então:
, então: 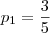 e, nesse caso, os termos da P.G. são:
e, nesse caso, os termos da P.G. são: 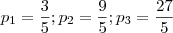
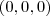 ou
ou 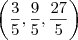 ou
ou 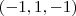

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: