Boa noite
É pra variar essas questões de PA, estão me deixando doida não consigo encontrar a saida para a questão, a principio parece facil, mas meu cerebro não consegue processar o desenvolvimento.
Uma seqüência de números (a1, a2, a3,...) é tal que a soma dos n primeiros termos é dada pela expressão Sn = 3n2 + n.
O valor do 51o termo é
(A) 300 (B) 301
(C) 302 (D) 303
(E) 304








 , e não cada elemento independente. Leia o enunciado atentamente:
, e não cada elemento independente. Leia o enunciado atentamente: é tal que a
é tal que a 
 você está calculando
você está calculando 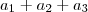 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
