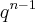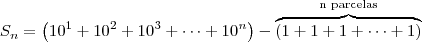por georgefdfdl » Qui Nov 10, 2011 23:49
por georgefdfdl » Qui Nov 10, 2011 23:49
''Calcule:
Sn=9+99+999+…+10n -1
Sabendo que se trata da soma dos termos de uma P.G.''
Eu sei sobre o termo geral de uma P.G. e como calcular com a formula do termo geral de uma P.G.(an=a1.
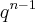
porem não estou conseguindo resolver esta questão, já que não consigo aplicar na formula, agradeço a quem puder me ajudar,
pois semana que vem haverá uma avaliação referente ao assunto e uma lista de exercicio.
-
georgefdfdl
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Nov 10, 2011 23:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sex Nov 11, 2011 17:41
por LuizAquino » Sex Nov 11, 2011 17:41
georgefdfdl escreveu:''Calcule:
Sn=9+99+999+…+10n -1
Sabendo que se trata da soma dos termos de uma P.G.''
Note que:


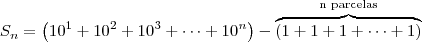
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calcule y
por Guilhermme » Sáb Mar 31, 2012 17:06
- 4 Respostas
- 4060 Exibições
- Última mensagem por Nico Romani

Qui Mar 31, 2016 17:01
Geometria Analítica
-
- Calcule a e b
por andersontricordiano » Dom Mar 02, 2014 12:01
- 3 Respostas
- 4659 Exibições
- Última mensagem por nat-larissa

Seg Mar 03, 2014 20:12
Sistemas de Equações
-
- Calcule
por andersontricordiano » Ter Mar 18, 2014 00:34
- 1 Respostas
- 1998 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 06, 2016 11:38
Aritmética
-
- Calcule f(x)
por kjelin » Ter Fev 02, 2016 01:39
- 1 Respostas
- 2712 Exibições
- Última mensagem por DanielFerreira

Seg Fev 08, 2016 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Calcule o 1º termo
 por Cleyson007 » Dom Dez 27, 2009 13:47
por Cleyson007 » Dom Dez 27, 2009 13:47
- 1 Respostas
- 2042 Exibições
- Última mensagem por Lucio Carvalho

Seg Dez 28, 2009 09:46
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.