 por rodsales » Dom Ago 30, 2009 10:23
por rodsales » Dom Ago 30, 2009 10:23
Simplificando a expressão (cos²x - cotgx)/sen²x - senx:
Fiz de todas maneiras possíveis não chegando a resultado nenhum.
Grato,
Aguardo respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Elcioschin » Dom Ago 30, 2009 10:37
por Elcioschin » Dom Ago 30, 2009 10:37
rodsales
1) Tem certeza do enunciado? Coloque o enunciado COMPLETO!!!
2) Qual é o denominador? É sen²x ou (sen²x - senx) ?
3) Se você diz que não conseguiu é porque sabe a resposta. Qual é a resposta ?
4) Existem alternativas ?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por rodsales » Dom Ago 30, 2009 10:48
por rodsales » Dom Ago 30, 2009 10:48
Vou escrever da mesma maneira que está no livro.
Simplificando a expressão (cos²x - cotgx)/(sen²x - tgx) , obtemos:
Resposta: cotg²x
Grato,
obs: nesse exercício está pedindo a identidade da expressão.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Lucio Carvalho » Dom Ago 30, 2009 11:16
por Lucio Carvalho » Dom Ago 30, 2009 11:16
Olá rodsales,
Apresento em seguida uma das possíveis simplificações por mim encontrada.
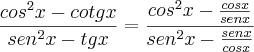


Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Elcioschin » Dom Ago 30, 2009 14:32
por Elcioschin » Dom Ago 30, 2009 14:32
rodsales
Espero que você tenha entendido como é importante colocar o enunciado COMPLETO e CORRETO!
Veja que você esqueceu de colocar os parenteses e trocou cotgx por senx no denominador e esqueceu de mostrar a resposta ou as alternativas.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatorial simplifique:
por natanskt » Ter Dez 07, 2010 13:36
- 3 Respostas
- 8047 Exibições
- Última mensagem por Molina

Ter Jun 28, 2011 20:27
Binômio de Newton
-
- Simplifique a expressão:
por andersontricordiano » Dom Jan 22, 2012 22:03
- 2 Respostas
- 7383 Exibições
- Última mensagem por laura1970

Ter Jun 11, 2013 10:50
Estatística
-
- Simplifique a Fração
por plugpc » Qui Mai 03, 2012 18:30
- 1 Respostas
- 1561 Exibições
- Última mensagem por DanielFerreira

Qui Mai 03, 2012 20:44
Sistemas de Equações
-
- [Potenciação] Simplifique
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:29
- 2 Respostas
- 1383 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:49
Álgebra Elementar
-
- simplifique as expressoes
por laura1970 » Seg Abr 22, 2013 16:03
- 3 Respostas
- 1762 Exibições
- Última mensagem por laura1970

Seg Abr 22, 2013 21:26
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





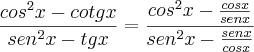




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.