 por Camila Z » Ter Jan 17, 2012 14:50
por Camila Z » Ter Jan 17, 2012 14:50
Sabendo que os lados de um triãngulo "não retângulo" medem
![3, \sqrt[]{3}, 2\sqrt[]{3} 3, \sqrt[]{3}, 2\sqrt[]{3}](/latexrender/pictures/89a1a9972e33d4b18ede1bdc51e9bf80.png)
, calcular os ângulos...
-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
 por ant_dii » Ter Jan 17, 2012 15:30
por ant_dii » Ter Jan 17, 2012 15:30
Uma saída é usar a lei dos cossenos, ou seja,



Neste caso, basta usar
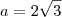
,
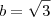
e

.
Lembre-se que

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Arkanus Darondra » Ter Jan 17, 2012 15:34
por Arkanus Darondra » Ter Jan 17, 2012 15:34
Camila Z escreveu:Sabendo que os lados de um triãngulo "não retângulo" medem
![3, \sqrt[]{3}, 2\sqrt[]{3} 3, \sqrt[]{3}, 2\sqrt[]{3}](/latexrender/pictures/89a1a9972e33d4b18ede1bdc51e9bf80.png)
, calcular os ângulos...
Olá Camila Z.
Basta utilizar a lei dos cossenos.

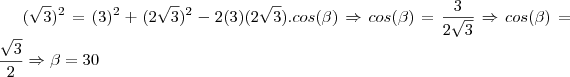

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Ter Jan 17, 2012 15:35
por Arkanus Darondra » Ter Jan 17, 2012 15:35
Desculpa ant_dii.
Não vi que a questão já havia sido respondida.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por ant_dii » Ter Jan 17, 2012 15:44
por ant_dii » Ter Jan 17, 2012 15:44
Sem problemas Arkanus, mas acho que o enunciado da questão da Camila esta errado, ou com algum problema, pois diz que o triângulo não é retângulo...
Camila, por favor, verifique o enunciado...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Camila Z » Ter Jan 17, 2012 16:09
por Camila Z » Ter Jan 17, 2012 16:09
Obrigada gente! O enunciado que me foi pedido é esse mesmo, deve estar errado... vou informá-los!

-
Camila Z
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Jan 16, 2012 22:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de Angulos
por gaspfamily » Dom Fev 12, 2012 17:32
- 1 Respostas
- 1596 Exibições
- Última mensagem por Arkanus Darondra

Dom Fev 12, 2012 18:07
Geometria Plana
-
- Cálculo de ângulos não-notáveis
por Francine » Seg Jun 11, 2012 18:05
- 1 Respostas
- 4242 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 18:35
Trigonometria
-
- Dúvida - cálculo de ângulos
por Danilo » Seg Jul 16, 2012 17:23
- 5 Respostas
- 2408 Exibições
- Última mensagem por Arkanus Darondra

Seg Jul 16, 2012 20:59
Trigonometria
-
- Calculo dos angulos internos dum triangulo hiperbólico
por Jhenrique » Ter Jul 24, 2012 18:42
- 0 Respostas
- 1819 Exibições
- Última mensagem por Jhenrique

Ter Jul 24, 2012 18:42
Geometria Espacial
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13568 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![3, \sqrt[]{3}, 2\sqrt[]{3} 3, \sqrt[]{3}, 2\sqrt[]{3}](/latexrender/pictures/89a1a9972e33d4b18ede1bdc51e9bf80.png) , calcular os ângulos...
, calcular os ângulos...

![3, \sqrt[]{3}, 2\sqrt[]{3} 3, \sqrt[]{3}, 2\sqrt[]{3}](/latexrender/pictures/89a1a9972e33d4b18ede1bdc51e9bf80.png) , calcular os ângulos...
, calcular os ângulos...



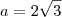 ,
, 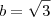 e
e  .
. .
.
, calcular os ângulos...









 , avisa que eu resolvo.
, avisa que eu resolvo.

