 por andersontricordiano » Seg Mar 07, 2011 19:24
por andersontricordiano » Seg Mar 07, 2011 19:24
Encontre o valor de x do triângulo abaixo:
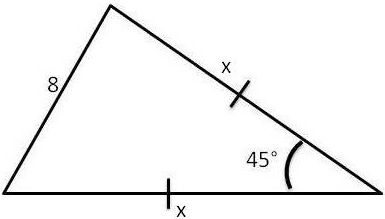
- triangulo1.jpg (10.29 KiB) Exibido 6257 vezes
Por favor me ajudem a encontrar o valor de x. Eu já tentei resolver esse exercício usando a formula da lei dos cossenos e não consigo chegar a resposta da qual é
10,45 aproximadamente Por favor onde foi que eu errei!
Obrigado quem tirar minha duvida!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mar 07, 2011 19:48
por LuizAquino » Seg Mar 07, 2011 19:48
andersontricordiano escreveu:Por favor me ajudem a encontrar o valor de x. Eu já tentei resolver esse exercício usando a formula da lei dos cossenos e não consigo chegar a resposta da qual é 10,45 aproximadamente
Por favor onde foi que eu errei!
Esse exercício pode ser resolvido usando a Lei dos Cossenos. Poste aqui o que você fez, desse modo podemos encontrar o erro.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por andersontricordiano » Seg Mar 07, 2011 20:05
por andersontricordiano » Seg Mar 07, 2011 20:05
fiz assim:
8²= x²+x²-2*x*x*cos45°
Fiz assim mais não consigo chegar a resposta!
está errado?
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mar 07, 2011 20:08
por LuizAquino » Seg Mar 07, 2011 20:08
andersontricordiano escreveu:fiz assim:
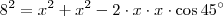
Fiz assim mais não consigo chegar a resposta!
está errado?
Você começou certo. Poste aqui o restante dos seus cálculos.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Pedro123 » Ter Mar 08, 2011 02:37
por Pedro123 » Ter Mar 08, 2011 02:37
Fala anderson, então cara, talvez, você tenha que usar valores aproximados, pelos calculos que fiz, você chegou em algo do tipo
![{x}^{2} = \frac{128 + 64.\sqrt[]{2}}{2} {x}^{2} = \frac{128 + 64.\sqrt[]{2}}{2}](/latexrender/pictures/a8147f8560bbcbc0b1a4f0ed9b8f1bd7.png)
tente trocar o
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
por um valor aproximado, algo proximo à
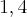
e você provavelmente encontrará a resposta.
abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UF-MG) Calcule o valor de A3/A2 do triângulo abaixo
 por andersontricordiano » Qua Mar 09, 2011 13:04
por andersontricordiano » Qua Mar 09, 2011 13:04
- 1 Respostas
- 2384 Exibições
- Última mensagem por andersontricordiano

Qua Mar 16, 2011 12:19
Geometria
-
- Encontre o valor de z
por manuoliveira » Ter Abr 22, 2014 15:53
- 2 Respostas
- 3038 Exibições
- Última mensagem por manuoliveira

Qua Abr 23, 2014 11:56
Números Complexos
-
- Encontre o valor de sen²x=1
por andersontricordiano » Seg Jul 18, 2011 12:48
- 3 Respostas
- 4519 Exibições
- Última mensagem por MarceloFantini

Seg Jul 18, 2011 21:18
Trigonometria
-
- (Calculo de logaritmo) Encontre o valor de y
por andersontricordiano » Qua Mar 23, 2011 13:39
- 1 Respostas
- 1982 Exibições
- Última mensagem por Molina

Qua Mar 23, 2011 15:07
Logaritmos
-
- Qual o valor de x no calculo abaixo
por andersontricordiano » Qui Mar 22, 2012 02:58
- 4 Respostas
- 6433 Exibições
- Última mensagem por Boyskoy89

Sex Out 28, 2016 05:31
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



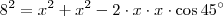
![{x}^{2} = \frac{128 + 64.\sqrt[]{2}}{2} {x}^{2} = \frac{128 + 64.\sqrt[]{2}}{2}](/latexrender/pictures/a8147f8560bbcbc0b1a4f0ed9b8f1bd7.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) por um valor aproximado, algo proximo à
por um valor aproximado, algo proximo à 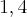 e você provavelmente encontrará a resposta.
e você provavelmente encontrará a resposta.