 por fernandocez » Qua Mar 02, 2011 11:26
por fernandocez » Qua Mar 02, 2011 11:26
Caro amigos do Forum, já olhei em dois livros e não achei nenhuma questão parecida que me dê uma luz. Parece simples mas não achei nenhuma relação entre eles. Fiz um desenho no plano, marquei os ângulos aproximados e mesmo assim não percebi a ligação. Aguardo uma ajuda dos amigos.
64. Sabendo que cos40º = 0,766, o valor de sen10º é:
resposta: 0,174
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qua Mar 02, 2011 12:12
por LuizAquino » Qua Mar 02, 2011 12:12
DicaVocê vai precisar das identidades trigonométricas:
(i)
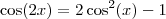
(ii)

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Sex Mar 04, 2011 00:59
por fernandocez » Sex Mar 04, 2011 00:59
Essa eu tô tentando tô chegando perto!
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Dom Mar 13, 2011 00:10
por fernandocez » Dom Mar 13, 2011 00:10
LuizAquino escreveu:DicaVocê vai precisar das identidades trigonométricas:
(i)
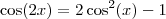
(ii)

Oi Luiz, eu tentei mas não cheguei a nenhum lugar. Vamos lá.
cos (2.40) = 2 cos² (40) - 1 = cos (80) = 2(0,766)² - 1
cos 80 = 2.0,587 - 1 = cos 80 = 0,174
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Dom Mar 13, 2011 01:19
por LuizAquino » Dom Mar 13, 2011 01:19
Dica
Aplique a identidade (i) com x=20°. Com isso você irá calcular cos(20°).
Em seguida, aplique a mesma identidade para x=10°. Com isso você irá calcular cos(10°).
Por fim, use a identidade (ii) para calcular sen(10°).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Dom Mar 13, 2011 01:22
por Renato_RJ » Dom Mar 13, 2011 01:22
Fernando e Luiz, eu fiz usando outra propriedade trigonométrica, o cosseno/seno do arco metade...


Veja, se eu tenho o cosseno de 40º e quero o seno de 10º, primeiramente vou achar a metade de 40 e depois a metade de 20, veja:

Agora, vou achar o seno de 10º:
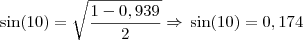
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Dom Mar 13, 2011 01:27
por LuizAquino » Dom Mar 13, 2011 01:27
Renato_RJ escreveu:Fernando e Luiz, eu fiz usando outra propriedade trigonométrica, o cosseno/seno do arco metade...
Essa é outra opção igualmente válida.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Dom Mar 13, 2011 01:31
por Renato_RJ » Dom Mar 13, 2011 01:31
Eu acabei achando essa relação em um livro que eu estava lendo hoje....
Mas se isso é questão de prova, essa prova deve ser bem chatinha, pois resolver essas raízes é bem enjoado....
Prof. Luiz, existe algum método para fatoração mais simples ou essas raízes tem que ser feitas no "velho método braçal" ?
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Dom Mar 13, 2011 01:46
por LuizAquino » Dom Mar 13, 2011 01:46
Renato_RJ escreveu:Prof. Luiz, existe algum método para fatoração mais simples ou essas raízes tem que ser feitas no "velho método braçal" ?
Existem algoritmos para o cálculo de raiz quadrada. Leia a respeito na Wikipédia:
Raiz quadradahttp://pt.wikipedia.org/wiki/Raiz_quadrada
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Dom Mar 13, 2011 03:33
por MarceloFantini » Dom Mar 13, 2011 03:33
Eu prefiro o algoritmo da calculadora, pessoalmente. Sobre o exercício:

Sua resolução estava certa. Existem vários jeitos de resolver a questão: o seu (calculando 80 e usando o fato que eu mostrei), fazendo duas divisões usando as contas que o Luiz Aquino sugeriu ou usando a fórmula decorada do Renato (que na verdade é uma equivalente à do Luiz, porém extraindo somente a raíz positiva ele elimina ângulos do 2° e 3° quadrantes; como o exercício já definia o primeiro isto não causava problemas, mas é bom lembrar).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Renato_RJ » Dom Mar 13, 2011 03:41
por Renato_RJ » Dom Mar 13, 2011 03:41
Poxa Fantini, "fórmula decorada" doeu no coração.. kkkkkkkkkkkkkk...........
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por MarceloFantini » Dom Mar 13, 2011 03:51
por MarceloFantini » Dom Mar 13, 2011 03:51
Foi mal, não era a intenção...hauhauhahua.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Dom Mar 13, 2011 11:23
por LuizAquino » Dom Mar 13, 2011 11:23
Fantini escreveu:Sobre o exercício:
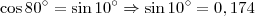
Eis outra opção igualmente válida.
ObservaçãoApenas para alertar os incautos, esta solução usa a relação entre ângulos complementares:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Dom Mar 13, 2011 12:18
por fernandocez » Dom Mar 13, 2011 12:18
Obrigado pessoal, consegui fazer a questão. Tenho que estudar mais trigonometria e também os outros assuntos.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3555 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1823 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2672 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
-
- Questão prova concurso prbabilidade
por fernandocez » Ter Mar 01, 2011 12:44
- 2 Respostas
- 1733 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:50
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



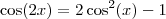








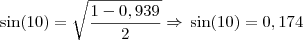









 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

