![[1,1+\frac{3\sqrt{3}}{4}] [1,1+\frac{3\sqrt{3}}{4}]](/latexrender/pictures/5a1cdd9fa2d6036b83a7d58726f07f8c.png) .
.Em relação à alínea e, fiz assim:

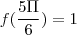
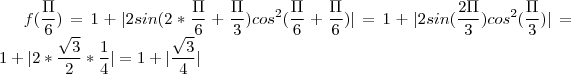


![[1,1+\frac{3\sqrt{3}}{4}] [1,1+\frac{3\sqrt{3}}{4}]](/latexrender/pictures/5a1cdd9fa2d6036b83a7d58726f07f8c.png) .
.
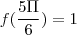
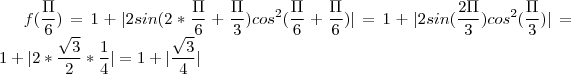


 (Basta desenvolver sin(a+b) =sin(a)cos(b) + sin(b)cos(b) para o caso em que a=b) para qualquer
(Basta desenvolver sin(a+b) =sin(a)cos(b) + sin(b)cos(b) para o caso em que a=b) para qualquer  .
.  e assim ,
e assim ,  . Logo teremos
. Logo teremos ![sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*) sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*)](/latexrender/pictures/64e37509b2c53492d470ac4b2d577c81.png) .
.  .
. 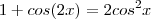 .
.  e além disso
e além disso  do domínio de
do domínio de  , teremos
, teremos  e
e ![f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ] f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ]](/latexrender/pictures/d3a6351590d1e88d2f1bc3c2d51d6d8b.png) . O contradomínio de f é qualquer conjunto que contém o intervalo acima , podendo ser o próprio intervalo .
. O contradomínio de f é qualquer conjunto que contém o intervalo acima , podendo ser o próprio intervalo .
 :
:
![sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x](/latexrender/pictures/deb319e8d001fe8f0b65b42a75b8a721.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: