 por e8group » Qua Abr 02, 2014 10:19
por e8group » Qua Abr 02, 2014 10:19
Bom dia !
Segestão :
a)
Note que

(Basta desenvolver sin(a+b) =sin(a)cos(b) + sin(b)cos(b) para o caso em que a=b) para qualquer

.
Agora

e assim ,

. Logo teremos
![sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*) sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*)](/latexrender/pictures/64e37509b2c53492d470ac4b2d577c81.png)
.
Mas , sabemos que

.
Usando a fórmula acima tente mostrar que
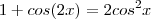
.
e)
vc desenvolveu corretamente , agora lembre-se que

e além disso
f(x) se relaciona por 1 + "número positivo" , quando este número "positivo" for máximo , f(x) também será . Analogamente, quando este "número positivo" for mínimo , f(x) tbm será . Ora, então para qualquer ponto

do domínio de

, teremos

e
![f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ] f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ]](/latexrender/pictures/d3a6351590d1e88d2f1bc3c2d51d6d8b.png)
. O contradomínio de f é qualquer conjunto que contém o intervalo acima , podendo ser o próprio intervalo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fff » Qua Abr 02, 2014 10:33
por fff » Qua Abr 02, 2014 10:33
Obrigada pela explicação!!
Eu tenho a fórmula do

:

Então:
![sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x](/latexrender/pictures/deb319e8d001fe8f0b65b42a75b8a721.png)
-

fff
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sáb Dez 21, 2013 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Informática
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6558 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11344 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15298 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4420 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3369 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[1,1+\frac{3\sqrt{3}}{4}] [1,1+\frac{3\sqrt{3}}{4}]](/latexrender/pictures/5a1cdd9fa2d6036b83a7d58726f07f8c.png) .
.
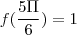
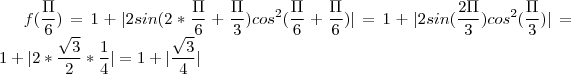


![[1,1+\frac{3\sqrt{3}}{4}] [1,1+\frac{3\sqrt{3}}{4}]](/latexrender/pictures/5a1cdd9fa2d6036b83a7d58726f07f8c.png) .
.
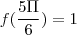
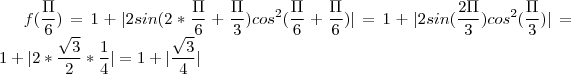


 (Basta desenvolver sin(a+b) =sin(a)cos(b) + sin(b)cos(b) para o caso em que a=b) para qualquer
(Basta desenvolver sin(a+b) =sin(a)cos(b) + sin(b)cos(b) para o caso em que a=b) para qualquer  .
.  e assim ,
e assim ,  . Logo teremos
. Logo teremos ![sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*) sin(2x) + sin(4x)/2 = sin(2x) + sin(2x)cos(2x) = sin(2x)[1 + cos(2x)] (*)](/latexrender/pictures/64e37509b2c53492d470ac4b2d577c81.png) .
.  .
. 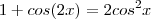 .
.  e além disso
e além disso  do domínio de
do domínio de  , teremos
, teremos  e
e ![f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ] f(x) \leq 1 + \sqrt{3}/4 \therefore Im(f) \subset [1 ,1 + \sqrt{3}/4 ]](/latexrender/pictures/d3a6351590d1e88d2f1bc3c2d51d6d8b.png) . O contradomínio de f é qualquer conjunto que contém o intervalo acima , podendo ser o próprio intervalo .
. O contradomínio de f é qualquer conjunto que contém o intervalo acima , podendo ser o próprio intervalo .
 :
:
![sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x sin(2x)[1+cos(2x)]=sin(2x)[1+cos^2x-sin^2x]=sin(2x)[1-sin^2x+cos^2x]=sin(2x)[cos^2x+cos^2x]=sin(2x)[2cos^2x]=2sin(2x)cos^2x](/latexrender/pictures/deb319e8d001fe8f0b65b42a75b8a721.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.