 por estudandoMat » Qua Abr 07, 2010 02:15
por estudandoMat » Qua Abr 07, 2010 02:15
Calcular seno(22,5)°
To aqui me matando pra tenta fazer isso x_x . Sei q n eh complicado, mas n consigo pensar numa maneira de desmembrar. Ja tentei seno(45-22,5). Tb seno(45/2) (esse eu so montei, mas n sei a regra pra divisao, que nem tem na apostila)
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Lucio Carvalho » Qua Abr 07, 2010 08:50
por Lucio Carvalho » Qua Abr 07, 2010 08:50
Olá estudandoMat,
Vou ajudar-te, pegando na tua segunda ideia, isto é, sin 22,5º = sin (45/2)º.
Mas, primeiramente explicarei como podemos obter a fórmula para a bissecção do ângulo para o seno.
Sabemos que,

Então,

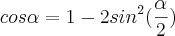
![sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}} sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}}](/latexrender/pictures/6c98d275d5d8f2fc0047e833ced5d3ca.png)
Agora é só calcular:
![sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=... sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=...](/latexrender/pictures/64688d8fb6822d41b2581c14af5c3752.png)
Também podes obter as fórmulas de bissecção do ângulo para o cos e a tg. São elas:
![cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}} cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}}](/latexrender/pictures/fd14e92b142aaf3e6b8366eec580d3af.png)
![tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}} tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}}](/latexrender/pictures/907e830076c22870ce9e3ef528694520.png)
Espero ter ajudado!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por estudandoMat » Qua Abr 07, 2010 10:59
por estudandoMat » Qua Abr 07, 2010 10:59
Obrigado pelas fórmulas, Lucio!
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Seno 1
por estudandoMat » Dom Abr 04, 2010 21:02
- 4 Respostas
- 4731 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 00:27
Trigonometria
-
- Seno de -?/2
por samra » Sáb Mar 10, 2012 09:34
- 2 Respostas
- 1694 Exibições
- Última mensagem por samra

Sex Mar 30, 2012 00:04
Trigonometria
-
- Limite de seno x
por luiz3107 » Seg Jun 21, 2010 13:55
- 2 Respostas
- 3709 Exibições
- Última mensagem por MarceloFantini

Ter Jun 22, 2010 01:43
Cálculo: Limites, Derivadas e Integrais
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4656 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18808 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




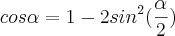
![sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}} sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}}](/latexrender/pictures/6c98d275d5d8f2fc0047e833ced5d3ca.png)
![sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=... sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=...](/latexrender/pictures/64688d8fb6822d41b2581c14af5c3752.png)
![cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}} cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}}](/latexrender/pictures/fd14e92b142aaf3e6b8366eec580d3af.png)
![tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}} tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}}](/latexrender/pictures/907e830076c22870ce9e3ef528694520.png)


 .
.
 :
: