 por Fontelles » Ter Dez 29, 2009 10:04
por Fontelles » Ter Dez 29, 2009 10:04
Para que valores de x está definida a função?
![f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}}](/latexrender/pictures/a1c32887b97686edf4ab7882c9defb5e.png)
Rapaz, acho que pra resolver isso tem que achar um termo em comum, mas nem isso eu tô conseguindo fazer.
Tentei de outra forma, considerando que sen2x-2 será sempre < 0, independente do valor de x, então para definir a equação o divisor deveria ser < 0 também, mas não cheguei em uma resposta satisfatória com o gabarito.
Ajuda ae, pessoal!
-
Fontelles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Dez 09, 2009 01:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Ter Dez 29, 2009 15:51
por Marcampucio » Ter Dez 29, 2009 15:51
O radicando do numerador tem de ser maior ou igual a zero

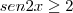
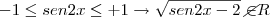
a equação não tem solução Real.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Fontelles » Ter Dez 29, 2009 19:04
por Fontelles » Ter Dez 29, 2009 19:04
Pior que não é essa a resposta, cara.
Acho que como o numerador vai sempre dar negativo, o divisor também tem de ser negativo para a raíz poder existir.
-
Fontelles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Dez 09, 2009 01:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Ter Dez 29, 2009 19:33
por Marcampucio » Ter Dez 29, 2009 19:33
Fontelles escreveu:Para que valores de x está definida a função?
![f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}}](/latexrender/pictures/a1c32887b97686edf4ab7882c9defb5e.png)
Rapaz, acho que pra resolver isso tem que achar um termo em comum, mas nem isso eu tô conseguindo fazer.
Tentei de outra forma, considerando que sen2x-2 será sempre < 0, independente do valor de x, então para definir a equação o divisor deveria ser < 0 também, mas não cheguei em uma resposta satisfatória com o gabarito.
Ajuda ae, pessoal!
só prá conferir:
a coisa é
![f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}}](/latexrender/pictures/a1c32887b97686edf4ab7882c9defb5e.png)
ou é
![f(x) = \frac{\sqrt[]{sen^2x - 2}}{\sqrt[]{cos^2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen^2x - 2}}{\sqrt[]{cos^2x + 3cosx - 1}}](/latexrender/pictures/81e1b063f9dc0024a5b3e74005512b91.png)
na primeira forma não tem jeito mesmo, o numeradorr não é Real.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por rvitorper » Qui Mar 17, 2011 16:25
por rvitorper » Qui Mar 17, 2011 16:25
Vi em um livro a seguinte forma para f(x):
![f(x) = \sqrt[2]{\frac{sen 2x - 2}{cos 2x + 3cos x - 1}} f(x) = \sqrt[2]{\frac{sen 2x - 2}{cos 2x + 3cos x - 1}}](/latexrender/pictures/a8ddeb7d11e727ec39cbfafb9124502d.png)
Dessa maneira é fácil resolver. Dado que o antecedente é menor que 0, o consequente deve ser menor que 0 também para que f(x) tenha domínio real:
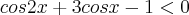
O que nos dá:
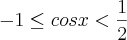
Por fim:
![D = \left[ x \epsilon \Re / \frac{\pi}{3} < x < \frac{5\pi}{3} \right] D = \left[ x \epsilon \Re / \frac{\pi}{3} < x < \frac{5\pi}{3} \right]](/latexrender/pictures/81c4ad625409c8efcb9fa3455fbaef5c.png)
-
rvitorper
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 17, 2011 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qui Mar 17, 2011 17:49
por Elcioschin » Qui Mar 17, 2011 17:49
Fontelles
Quando você postar uma questão e souber a resposta, por favor POSTE-A também.
Isto facilita a vida de quem pretende ajudá-lo.
O caminho do rvitorper (de colocar tudo dentro de um mesmo radical) é o caminho correto.
Vou apenas detalhá-lo um pouco mais:
1) O numerador (sen2x - 2) é sempre negativo
2) Para se ter uma radicando POSITIVO o denominador deverá ser NEGATIVO, isto é:
cos2x + 3cosx - 1 < 0
(2*cos²x - 1) + 3cosx - 1 < 0
2cos²x + 3cosx - 2 < 0 ----> O primeiro membro é uma parábola vom a concavidade voltada para cima (a = 2)
Para esta função ser NEGATIVA cosx deve estar situada entre as raízes
Discriminante ----> D = b² - 4ac ---> D = 3² - 4*2*(-2) ---> D = 25 ----> V(D) = 5
Raízes: cosx = - 2 e cosx = 1/2
Acontece que -1 < cos x < + 1
Solução - 1 < cos x < 1/2 ----> pi/3 < x < 5pi/3 ---> Exatamente a solução do rvitorper
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determine o valor de L para que a função
por Ana Maria da Silva » Qui Mai 09, 2013 12:11
- 0 Respostas
- 1185 Exibições
- Última mensagem por Ana Maria da Silva

Qui Mai 09, 2013 12:11
Cálculo: Limites, Derivadas e Integrais
-
- Determine o valor de k para que a função seja contínua...
por igorsantana2005 » Sex Abr 12, 2013 17:30
- 1 Respostas
- 8489 Exibições
- Última mensagem por e8group

Sex Abr 12, 2013 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Definida] Está certa minha resolução?
por Fabio Wanderley » Seg Out 22, 2012 23:37
- 2 Respostas
- 2029 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:45
Cálculo: Limites, Derivadas e Integrais
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3246 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- Ajuda para resolver Integral definida
por rodolphogagno » Qua Dez 01, 2010 15:16
- 4 Respostas
- 3575 Exibições
- Última mensagem por Moura

Seg Dez 13, 2010 21:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen2x - 2}}{\sqrt[]{cos2x + 3cosx - 1}}](/latexrender/pictures/a1c32887b97686edf4ab7882c9defb5e.png)



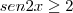
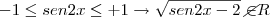 a equação não tem solução Real.
a equação não tem solução Real.
![f(x) = \frac{\sqrt[]{sen^2x - 2}}{\sqrt[]{cos^2x + 3cosx - 1}} f(x) = \frac{\sqrt[]{sen^2x - 2}}{\sqrt[]{cos^2x + 3cosx - 1}}](/latexrender/pictures/81e1b063f9dc0024a5b3e74005512b91.png)
![f(x) = \sqrt[2]{\frac{sen 2x - 2}{cos 2x + 3cos x - 1}} f(x) = \sqrt[2]{\frac{sen 2x - 2}{cos 2x + 3cos x - 1}}](/latexrender/pictures/a8ddeb7d11e727ec39cbfafb9124502d.png)
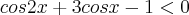
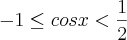
![D = \left[ x \epsilon \Re / \frac{\pi}{3} < x < \frac{5\pi}{3} \right] D = \left[ x \epsilon \Re / \frac{\pi}{3} < x < \frac{5\pi}{3} \right]](/latexrender/pictures/81c4ad625409c8efcb9fa3455fbaef5c.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
