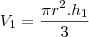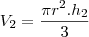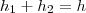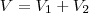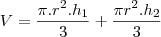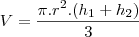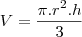por rochadapesada » Qua Abr 24, 2013 17:57
por rochadapesada » Qua Abr 24, 2013 17:57
Um dos catetos de um triângulo retângulo
mede
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
. O volume do sólido gerado pela
rotação deste triângulo em torno da hipotenusa é

cm¤. Determine os ângulos deste triângulo.
Fiz a rotação, percebi que forma 2 cones, mas dai travei
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Abr 25, 2013 13:08
por young_jedi » Qui Abr 25, 2013 13:08
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Qui Abr 25, 2013 22:38
por rochadapesada » Qui Abr 25, 2013 22:38
Eu só não entendi como você fez para usar apenas um volume, pois do jeito que estudo, do jeito que o professor explicou e do jeito que está em todos os livros que eu vejo, tem que temos que ter 2 volumes, ex: Volume total é igual a volume do pequeno cone + o volume do cone grande... do jeito que você fez, apenas usou apenas 1 volume para igualar com

... Tem alguma coisa a ver com a relação que você fez?
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por rochadapesada » Qui Abr 25, 2013 23:20
por rochadapesada » Qui Abr 25, 2013 23:20
É mesmo, Valeu =D... cara se puder responder, eu vou vou fazer uma prova de vestibular no meio do ano, ai eu estou fazendo diversas questões, mas eu sempre me pergunto: é melhor fazer questões do ITA, IME (de provas muito dificeis) ou faço questões da minha universidade que é razoável? Oque você me diz?
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Abr 25, 2013 23:26
por young_jedi » Qui Abr 25, 2013 23:26
o lado bom de resolver as questões do ime e do ita, é que se voce tiver conseguindo resolver estas questões dificilmente vai ter algo que te surpreenda na prova, mais por outro lado o bom de voce resolver as questões da universidade que voce quer é que voce se acostuma com o estilo da prova então voce ja chega la tendo uma ideia de como vai ser, do tempo medio que voce leva para responder uma questão.
Em resumo eu aconselharia voce se dedicar a estudar as questões da universidade que voce quer, se focar nas provas destas, mais quando tiver um tempo livre, um tempo extra do seu horario de estudos normal tambem resolver estas quetões de vestibulares mais dificeis.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de Triângulo Retângulo
 por mony0771 » Ter Abr 21, 2009 17:05
por mony0771 » Ter Abr 21, 2009 17:05
- 2 Respostas
- 1959 Exibições
- Última mensagem por mony0771

Qua Abr 22, 2009 09:16
Geometria Analítica
-
- [Triangulo retangulo] Exercicio duvida
por tuffy1 » Sáb Ago 25, 2012 18:35
- 5 Respostas
- 2881 Exibições
- Última mensagem por tuffy1

Dom Ago 26, 2012 18:40
Trigonometria
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4034 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Questão sobre triângulo incentro
 por LuizCarlos » Dom Abr 01, 2012 19:00
por LuizCarlos » Dom Abr 01, 2012 19:00
- 4 Respostas
- 7420 Exibições
- Última mensagem por LuizCarlos

Dom Abr 01, 2012 20:49
Trigonometria
-
- Dúvida sobre a questão
por thiago vestibular » Dom Jul 13, 2014 00:03
- 3 Respostas
- 3602 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 22:29
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) . O volume do sólido gerado pela
. O volume do sólido gerado pela 

![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) . O volume do sólido gerado pela
. O volume do sólido gerado pela 

![\frac{r}{\sqrt[3]2}=\frac{x}{h} \frac{r}{\sqrt[3]2}=\frac{x}{h}](/latexrender/pictures/f6301daa4515fa9e949302ac78c02c7b.png)
![r=\frac{\sqrt[3]2x}{h} r=\frac{\sqrt[3]2x}{h}](/latexrender/pictures/7a24903437e8fd572b22006af915d47c.png)
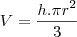
![\pi=\frac{h\pi}{3}.\frac{\sqrt[3]2^2.x^2}{h^2} \pi=\frac{h\pi}{3}.\frac{\sqrt[3]2^2.x^2}{h^2}](/latexrender/pictures/f7300efaaa9e5978e6a37a5255f26cbe.png)
![3h=\sqrt[3]2^2.x^2 3h=\sqrt[3]2^2.x^2](/latexrender/pictures/fb385d97ed8828fe1d0deed2a4a3d5bc.png)
![x^2=h^2-\sqrt[3]{2}^2 x^2=h^2-\sqrt[3]{2}^2](/latexrender/pictures/d0562d01e6e9fbe370a5fffcb78e32fa.png)
![3h=\sqrt[3]2^2.(h^2-\sqrt[3]{2}^2) 3h=\sqrt[3]2^2.(h^2-\sqrt[3]{2}^2)](/latexrender/pictures/efa2ca9cce2bc986caaa74742332102a.png)
![\sqrt[3]2^2h^2-3h-2\sqrt[3]{2}=0 \sqrt[3]2^2h^2-3h-2\sqrt[3]{2}=0](/latexrender/pictures/5348925eb9dd681155ee97ffccaec33f.png)
![h=\frac{4}{\sqrt[3]2^2} h=\frac{4}{\sqrt[3]2^2}](/latexrender/pictures/0ecb537acf45861485934d95976c6ed9.png)
![h=2\sqrt[3]2 h=2\sqrt[3]2](/latexrender/pictures/d584215ca5e8e89d4f597e8ca022dc5e.png)

 ... Tem alguma coisa a ver com a relação que você fez?
... Tem alguma coisa a ver com a relação que você fez?