 por Sabrinna » Qui Abr 04, 2013 18:48
por Sabrinna » Qui Abr 04, 2013 18:48
Estou novamente enroscada nessa outra questão...

Se cos x= -3/5 e ? ? x ? 3 ? /2, determine:
sen 2x..............cos 2x............tg 2x
-
Sabrinna
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Abr 04, 2013 15:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Abr 04, 2013 21:46
por e8group » Qui Abr 04, 2013 21:46
Foi dado
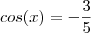
e
![x\in[\pi, 3\cdot \frac{\pi}{2}] x\in[\pi, 3\cdot \frac{\pi}{2}]](/latexrender/pictures/2b7c4c02151e8fb7de3261bd949af6c0.png)
.
Queremos calcular ,
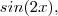
cos(2x) [/tex] e
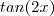
.
Note que
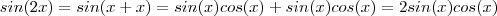
.
Mas, sabemos que pela identidade trigonométrica fundamental

,então
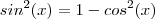
e como
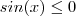
para todo x em
![[\pi, 3\cdot \frac{\pi}{2}] [\pi, 3\cdot \frac{\pi}{2}]](/latexrender/pictures/d446691ca0f56b5dbae21a32e129fd47.png)
obtemos que
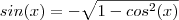
. Assim ,
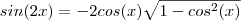
.Já
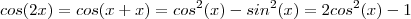
.Basta substituir
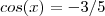
nas expressões obtidas .
Tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sabrinna » Qui Abr 04, 2013 22:49
por Sabrinna » Qui Abr 04, 2013 22:49
Parece confuso,mas com tua explicação deu para esclarecer um pouco.Vou refazer.Obrigada por tudo!

-
Sabrinna
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Abr 04, 2013 15:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Trigonometria no ciclo]
por Sabrinna » Qui Abr 04, 2013 16:04
- 2 Respostas
- 1520 Exibições
- Última mensagem por Sabrinna

Qui Abr 04, 2013 18:44
Trigonometria
-
- [Trigonometria no ciclo]
por Sabrinna » Sáb Abr 06, 2013 20:41
- 5 Respostas
- 3019 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:37
Trigonometria
-
- [Trigonometria no ciclo]
por Sabrinna » Dom Abr 07, 2013 23:41
- 3 Respostas
- 1718 Exibições
- Última mensagem por e8group

Seg Abr 08, 2013 16:24
Trigonometria
-
- [trigonometria no ciclo]
por Cido Almeida » Ter Abr 09, 2013 02:41
- 0 Respostas
- 1039 Exibições
- Última mensagem por Cido Almeida

Ter Abr 09, 2013 02:41
Trigonometria
-
- ciclo
por Apotema » Seg Nov 23, 2009 14:06
- 2 Respostas
- 1398 Exibições
- Última mensagem por Apotema

Seg Nov 23, 2009 14:52
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




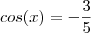 e
e ![x\in[\pi, 3\cdot \frac{\pi}{2}] x\in[\pi, 3\cdot \frac{\pi}{2}]](/latexrender/pictures/2b7c4c02151e8fb7de3261bd949af6c0.png) .
.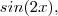 cos(2x) [/tex] e
cos(2x) [/tex] e 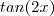 .
. 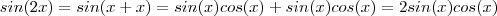 .
.  ,então
,então 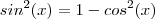 e como
e como 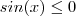 para todo x em
para todo x em ![[\pi, 3\cdot \frac{\pi}{2}] [\pi, 3\cdot \frac{\pi}{2}]](/latexrender/pictures/d446691ca0f56b5dbae21a32e129fd47.png) obtemos que
obtemos que 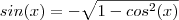 . Assim ,
. Assim , 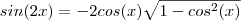 .Já
.Já 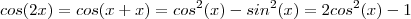 .Basta substituir
.Basta substituir 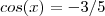 nas expressões obtidas .
nas expressões obtidas . 


