 por Justiceira » Dom Set 27, 2009 13:33
por Justiceira » Dom Set 27, 2009 13:33
Pq com essa resolução resolverei outros exercicios parecidos
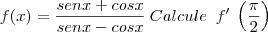
Me Ajudem por favor
-

Justiceira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 27, 2009 12:26
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Dom Set 27, 2009 14:53
por Cleyson007 » Dom Set 27, 2009 14:53
Boa tarde "Justiceira"!
Primeiramente, seja bem vinda ao Ajuda Matemática!
Não tenho certeza se estou certo.... mas, eu faria assim:

Note que

--> 90º


Logo,
 Resposta: 1
Resposta: 1Tem o gabarito da questão?
Até mais.
Espero ter ajudado.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Dom Set 27, 2009 16:54
por Cleyson007 » Dom Set 27, 2009 16:54
Justiceira escreveu:O gabarito seria esse

Passado pelo professor ,mas não consigo chegar a esse resultado

Olá, boa tarde!
Não encontrei erro em minha resolução..

Vamos ver o que os outros usuários do fórum dizem

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Galera preciso de ajuda urgente mesmo
por Dankaerte » Qua Ago 26, 2009 16:49
- 5 Respostas
- 3608 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 18:04
Polinômios
-
- [logica] resolução dessa questão
por amanda s » Sáb Nov 16, 2013 09:58
- 1 Respostas
- 1536 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 11:02
Lógica
-
- Qual a resolução dessa questão?
por NOShotgun » Sáb Dez 14, 2013 02:54
- 0 Respostas
- 1950 Exibições
- Última mensagem por NOShotgun

Sáb Dez 14, 2013 02:54
Lógica
-
- Preciso da Resolução desse exercicio
por alexcaju » Sex Jan 17, 2014 19:58
- 0 Respostas
- 1067 Exibições
- Última mensagem por alexcaju

Sex Jan 17, 2014 19:58
Matemática Financeira
-
- preciso de orientaçao para resoluçao(polinomios)
por Fabricio dalla » Ter Abr 05, 2011 17:19
- 3 Respostas
- 2813 Exibições
- Última mensagem por Elcioschin

Qua Abr 06, 2011 09:23
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
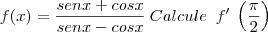

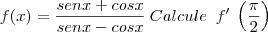


 --> 90º
--> 90º

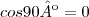







 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.